Trasmissione del calore

TRASMISSIONE DEL CALORE

Es.1       Un tubo sospeso orizzontalmente trasporta nafta attraverso un ampio locale. Valutare, in relazione ai dati riportati di seguito, il rapporto tra la potenza termica dispersa dal tubo per convezione e quella dispersa per irraggiamento.

- temperatura dell'aria: 15,0 °C;

- temperatura superficiale del tubo: 115 °C;

- temperatura media della superficie interna del locale: 10,0 °C;

- diametro esterno del tubo: 20,0 cm;

- emittenza della superficie del tubo, da considerare grigia: 0,870.

(0,800)

Es. 2      Una sottile piastra metallica quadrata, di 50,0 cm di lato è posta orizzontalmente in un vasto locale in cui la temperatura dell'aria è 16,0 °C e le pareti sono a 20 °C. Tutte le facce della piastra sono accuratamente coibentate tranne quella superiore, la cui temperatura è 616 °C. Questa temperatura è mantenuta per mezzo di riscaldamento elettrico, e la corrispondente potenza assorbita dalla rete è 5000 W. Si valuti l'emittenza della faccia non coibentata, assumendo per tutte le superfici un comportamento grigio.

(0,42)

Es. 3      Una lastra piana quadrata di acciaio inossidabile, di 1,45 m² di area e 1,00 cm di spessore, è disposta orizzontalmente in aria stagnante. La faccia inferiore è coibentata e si può considerare perfettamente adiabatica. La faccia superiore è esposta al sole e può essere considerata grigia con un'emittenza di 0,500. Se la temperatura della faccia superiore della piastra è 60,0 °C e la temperatura dell'aria è 16,0 °C, si calcolino:

a) il flusso solare incidente;

b) la temperatura della faccia inferiore della piastra.

(1,20 kW/m²; 60,0 °C)

Es. 4      Un elemento scaldante a simmetria cilindrica del diametro di 18,0 mm, collocato in un vasto ambiente con pareti a 20,0 °C ed aria stagnante alla stessa temperatura, è riscaldato internamente da una resistenza elettrica percorsa da corrente e a regime permanente raggiunge una temperatura superficiale di 834°C. Calcolare la potenza elettrica che va fornita ad ogni metro dell'elemento scaldante per le seguenti condizioni di funzionamento:

- temperatura dell'aria e delle pareti dell'ambiente 20,0°C;

- disposizione rettilinea ed orizzontale;

- emittenza superficiale dell'elemento (grigio) 0,900.

(5,00 kW/m)

Es. 5      Una sottile lastra di rame, riscaldata da una resistenza elettrica (R = 20,0 W m²), da un lato è a contatto con una parete in muratura e dall'altro perfettamente coibentata. La parete in muratura, dal lato non a contatto con la lastra di rame, è irraggiata con una potenza termica incidente di 800 W/m² ed è a contatto con un fluido alla temperatura di -20,0°C con un coefficiente convettivo di 15,0 W/m²K. Si calcoli il valore della corrente che deve attraversare la resistenza elettrica affinché la temperatura superficiale della parete in muratura irraggiata sia pari a 27,0°C, il coefficiente di assorbimento di questa parete sia 0,750 e l'emittenza 0,880.

(5,00 A)

Es. 6      Relativamente allo schema raffigurato si ritengono noti i seguenti dati:

- le sup. 1 e 2 sono piane, indefinite e grigie, e sono separate dal vuoto: la loro emittenza è pari a 0,280;

- t₂ = 320 °C;

- il materiale costituente la parete 2-3 è ferro, e lo spessore è 0,540 cm;

- il materiale costituente la parete 3-4 è amianto, e lo spessore è di 0,500 cm;

- la parete 4 è a contatto con aria (T = 10,0 °C), e la conduttanza unitaria superficiale totale (convez. + irraggiamento) è di 58,0 W/ m²K. Calcolare il valore della temperatura superficiale T_1.

(904 K)

			Aria, T h4

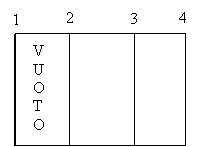
(N.B.: DA NON SVOLGERE PER TLC)

Es. 7 Un condotto di acciaio inossidabile lunga 130 m, di 5,00 cm di diametro interno e 4,00 mm di spessore, rivestito con uno strato di amianto dallo spessore di 4,00 cm, è attraversato da vapore d'acqua saturo a 2,00 bar, che entra con un titolo del 90,0% ed una portata volumetrica di 25,5 m³/h.. Le cadute di pressione nel condotto sono trascurabili. La condotta è sospesa in aria stagnante a 20,0 °C, e lo scambio radiativo superficiale può assumersi in prima approssimazione trascurabile. Anche la resistenza convettiva dal lato vapore è trascurabile (ovvero, la temperatura della parete interna del condotto è circa uguale a quella del vapore). Calcolare:

a)     la potenza termica complessivamente dispersa;

b)     il titolo del vapore in uscita.

Ai fini del calcolo del coefficiente di scambio convettivo superficiale, si assuma un valore ipotetico della superficie esterna del condotto pari a 50,0 °C, verificando poi la validità dell'ipotesi.

(12,8 kW, 0,25; temperatura della sup. esterna di circa 52 °C, ipotesi iniziale accettabile)

Es. 8 La superficie esterna di una barra cilindrica orizzontale (k=1,00 W/mK) di diametro esterno pari a 100 mm, grigia con emissività pari a 0,800, e di lunghezza pari a 1,00 m, deve disperdere una potenza termica pari a 157 W; la superficie esterna si trova a 120 °C.

Valutare, nell'ipotesi di regime stazionario monodimensionale, l'irradiazione G nelle ipotesi che la barra sia in aria stagnante con temperatura pari a 20,0 °C.

(N.B.: Regime non stazionario Ipotizzando quindi che i dati precedenti siano relativi all'istante iniziale di un transitorio termico, in assenza di generazione, ed assumendo inoltre che in questa fase la conduttanza termica unitaria h sia costante e pari al valore precedentemente calcolato per la sola convezione, determinare il tempo necessario affinché la temperatura minima del cilindro sia pari a 60,0°C. Si assuma a=9,00^.10^-7 m²/s

(1,65 kW/m², 3,5 10³ s)

Es. 9 In condizione di regime stazionario monodimensionale e con riferimento allo schema e ai dati di seguito riportati, si valutino:

i)   la conduttanza convettiva  per la superficie 4;

ii) la temperatura sulla superficie 1.

(1,40 kW/m²K, 200 °C)

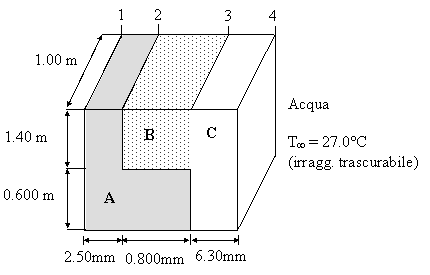
k_A = 5,00 W/mK;

materiale B = fibra di vetro;

materiale C = acciaio al manganese (1Mn);

T₄ = 93,0°C;

T = 27,0°C.

Es. 10  Nell'ipotesi si flusso monodimensionale e regime stazionario, ed assumendo che tutte le superfici siano grigie, si calcolino, per il sistema a simmetria cilindrica rappresentato in figura:

a)  la temperatura della superficie esterna dell'isolante, T₄;

b)  l'irradiazione sulla superficie esterna dell'isolante, G.

(120 °C, 2,9 kW/m²)

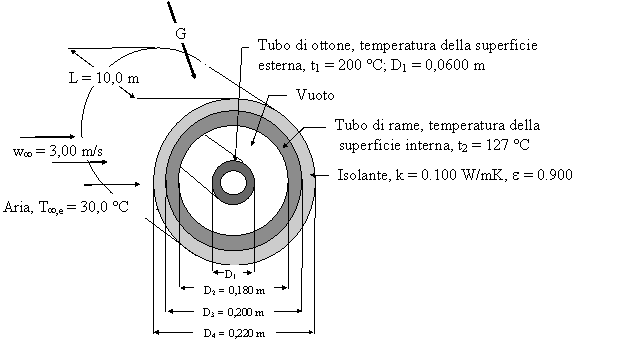
Es. 11    La parete schematizzata in figura separa un ambiente interno a 20,0 °C da uno esterno a 4,60°C. Attraverso la parete, alta 3,00 m, larga 5,00 m e spessa 23,0 cm e costituita dai materiali A, B e C, viene trasmessa una potenza termica pari a 131 W. Nell'ipotesi di stazionarietà e di monodimensionalità ed assumendo una conduttanza unitaria superficiale interna complessiva (convez. + irraggiamento) pari a h_a= 20,0 W/(m²K) si valutino:

a)  la temperatura della superficie 5;

b)  la conduttanza unitaria superficiale esterna complessiva (convez. + irraggiamento), h₅  .

(5,6 °C, 8,7 W/m²K)

Es. 12    In condizione di regime stazionario monodimensionale e con riferimento allo schema (nel quale è presente una cavità a due superfici) e ai dati di seguito riportati, si valuti :

a)     T₁;

b)     e

	kA = 0,197 W/(mK); T2 = 150°C; T3 = 180°C; e = e L >> H; r   = 0,500 m; s   = 0,0500 m; G = 300 W/m2; superfici grigie.

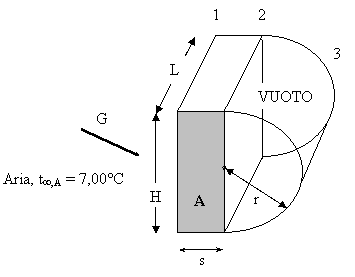(47,0°C, 0,661)

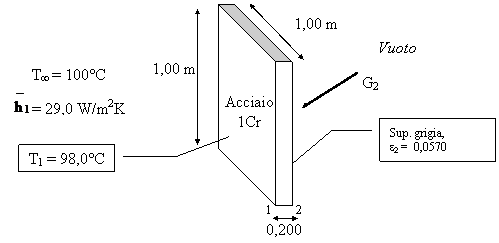
Es. 13  In relazione alla piastra rappresentata in figura, si calcolino, nell'ipotesi di regime stazionario monodimensionale:

a)     T₂;

b)     G₂.

(97,8°C, 54,3 W/m²)

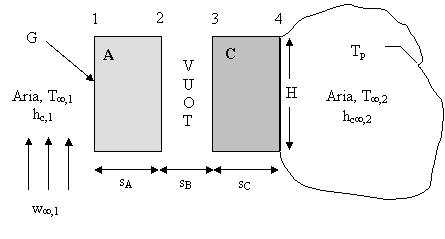
Es. 14  In relazione allo schema rappresentato in figura e ai dati riportati, ipotizzando che l'area di scambio sia quadrata e che la superficie 4 si affacci su un ambiente molto vasto con pareti isoterme alla temperatura T_p, si calcolino, nell'ipotesi di stazionarietà e di monodimensionalità:

a)     la conduttanza convettiva unitaria h

b)    

H = 4,00m; sA = 15,0 cm; sB << H; sC = 20,0 cm; T = -10,0°C; T4 = 25,0°C; T = Tp = 30,0°C; hc,2 = 3,00 Wm2/K; kA = 10,0 W/mK; kC = 5,00 W/mK; e1 e2 e3 e4 G = 548 W/m2; superfici grigie

la velocità w dell'aria che lambisce parallelamente la superficie 1.

(7,36 W/m²K, 2,7 m/s)

Es. 15  La struttura semicilindrica rappresentata in figura è immersa in un ambiente con aria a 5,0°C. la parete superiore 1 può considerarsi molto sottile, così come possono trascurarsi tutti gli effetti di bordo, essendo la dimensione nel piano ortogonale a quello di disegno, H = 20 m, molto maggiore di L, a sua volta molto maggiore di s. Si determini l'irradiazione G₃ relativa alla superficie 3.

T = 5,0°C; T1 = 25°C G1 = 200 W/m2; hc,1 = 2,0 W/m2K; k23 = 1.0 W/mK; e1 e2 e3 superfici grigie; H = 20 m; L = 1,0 m; s = 5,0 cm; (H = dimensione nella direzione ortogonale al piano di rappresentazione)

(1,8*10³ W/m²)

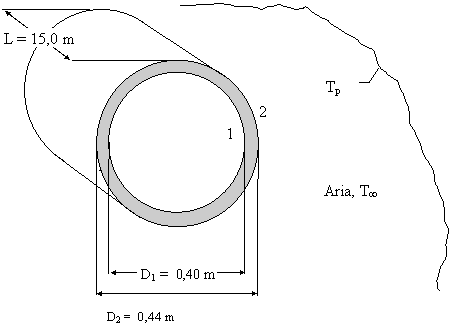
Es. 16 Un condotto molto lungo, costituito da pareti cilindriche coassiali 12 e 23, attraversa un vasto ambiente con pareti isoterme a 30 °C ed aria stagnante alla stessa temperatura. Ipotizzando condizioni di regime stazionario, e con riferimento ai dati in seguito riportati, determinare:

a)     la temperatura della superficie 2 (superficie di separazione tra le pareti cilindriche);

b)     la conducibilità termica k₂₃ della guaina cilindrica esterna.

(96 °C, 2,1 W/mK)

	t ,e = tp = 30 °C; t1 = 120 °C; t3 = 90 °C; k12 = 1,0 W/mK; e3 superfici grigie.

(N.B.: SOLO PER ALLIEVI GESTIONALI)

Es. 17 Un condotto percorso da vapore d'acqua saturo alla pressione costante di 2,0 bar, attraversa un vasto ambiente, con aria stagnante alla temperatura T = 30°C e pareti alla stessa temperatura, T = T_p.

Nell'attraversamento del condotto il vapore passa da un titolo iniziale pari a 1,0 ad uno finale pari a 0,98 a causa delle dispersioni termiche verso l'ambiente. Ipotizzando condizioni di regime stazionario, e con riferimento ai dati in seguito riportati, determinare:

a)     la conducibilità termica k della parete del condotto;

b)     l'emittenza e della superficie esterna del condotto (assunta grigia).

Inoltre assumendo per semplicità lo stesso valore della conduttanza superficiale complessiva relativo al caso precedente, si calcoli lo spessore d'isolante (conducibilità termica k' = 0,50 W/mK) necessario a ridurre le dispersioni termiche del 25%.

(1,8 W/mK, 0,63, 3,0 cm)

	vapore = 0,40 kg/s pin = pout = 2,0 bar; xin = 1,0; xout = 0,98; T = Tp = 30,0°C; T1-T2= 10°C; 2 = superficie grigia;

Es. 18 In relazione allo schema rappresentato in figura, si calcoli, nell'ipotesi di regime stazionario e di monodimensionalità del flusso termico conduttivo, la conduttanza convettiva media relativa alla superficie inferiore 4, assumendo trascurabile lo scambio convettivo relativo alla superficie superiore 1, e quello radiativo per la superficie

(42 W/m²K)

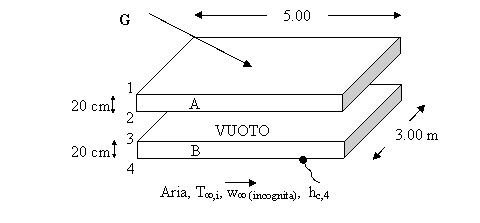
G = 350 W/m²;

materiale A = granito;

e₁

e₂ e₃

k_B = 10 W/mK;

T _,i = 93 °C;

T₁ = 50 °C;

superfici grigie

Es. La parete cilindrica delimitata dalle superfici 1 e 2 è circondata da uno schermo cilindrico coassiale molto sottile (superficie 3) che, a sua volta, attraversa un vasto ambiente delimitato dalla superficie  Nell'ipotesi di flusso monodimensionale e regime stazionario, si calcoli la temperatura della superficie

(18 °C)

Superfici 2, 3 e 4 grigie

Vuoto

e e

k₁₂ = 4,00 W/mK

w

t = 20 °C

w = 1,50 m/s

t₁ = 101 °C

t₂ = 100 °C

D₁ = 20,0 cm

D₂ = 22,0 cm

D₃ = 28,0 cm

L =5,00 m

A₄>>A₃

Es. In relazione allo schema rappresentato in figura, nel quale le pareti piane 1-2 e 2-3, a pianta quadrata, possono considerarsi sede di un campo di temperatura monodimensionale, e la superficie 4 è da considerarsi molto ampia rispetto alla 3, si calcolino, nell'ipotesi di regime stazionario:

a) il coefficiente di assorbimento della superficie 1, a₁

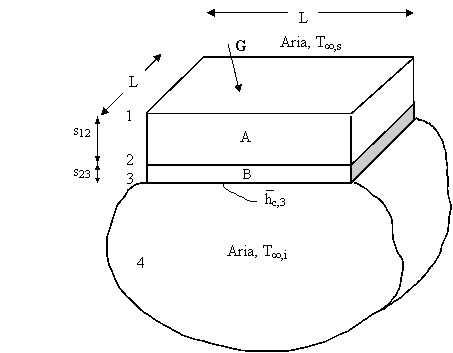b) la temperatura della superficie

(0,55, 31 °C)

T _,s = 30 °C;

T₁ = 50 °C;

T₃ = 35 °C;

e₁

G = 1000 W/m²;

k_A = 0,500 W/mK;

k_B = 0,200 W/mK;

superfici 3 e 4 grigie, e₃

h_c,3 = 1,50 W/m²K;

T _,i = 25 °C;

s₁₂ = 15,0 cm

s₂₃ = 5,00 cm

L = 5,00 m

A₄>>A₃

Es. Per il sistema schematizzato in figura, di profondità L = 10,0 m, si valuti, nell'ipotesi di regime stazionario, assumendo le superfici 3 e 4 parallele ed indefinite, ed utilizzando le consuete ipotesi semplificative il coefficiente di assorbimento della superficie 1, a