 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1990 | Gradito: |
Leggi anche appunti:Motore a combustione internaMotore a combustione interna Macchina termica motrice, in grado di trasformare ForzaForza Il termine forza è impiegato spesso in maniera impropria e senza Dimostrare sulla dilatazione volumica e lineare con degli esempi visti in laboratorioDimostrare sulla dilatazione volumica e lineare con degli esempi visti in laboratorio materiali |
 |
 |
Relatività Generale
Principio di Equivalenza.
Il principio di relatività ristretta era però ancora vincolato alla difficile definizione di un sistema di riferimento inerziale. Einstein riuscì a togliere a questa particolare classe di sistemi di riferimento la posizione di privilegio che era stata attribuita loro.
Già Galileo aveva notato che i corpi cadono con uguale accelerazione.
Dalla seconda legge della dinamica sappiamo che F = mi x a. La legge di gravitazione di Newton afferma che la forza di attrazione esercitata da un corpo di massa M è: F = mg x H, dove H è l'intensità del campo gravitazionale. Se a parità di H i corpi hanno tutti la stessa accelerazione, significa che mg/mi è costante. Scegliendo opportunamente le unità di misura si può fare in modo che tale rapporto valga uno. Attualmente è stato verificato sperimentalmente che la massa inerziale coincide con la massa gravitazionale con un errore di circa 10-13.
Questo fatto, noto come principio di equivalenza in forma debole, venne esteso da Einstein attraverso un esperimento ideale. Si consideri una navicella spaziale (Einstein usava un ascensore), al cui interno ci sia un laboratorio di fisica attrezzato per poter studiare il comportamento della materia senza poter osservare lo spazio esterno. L'esperimento viene descritto in quattro fasi: nella prima l'astronave viene posta in una regione dello spaziotempo priva di campi gravitazionali (quindi lontana da qualsiasi corpo celeste) e lasciato andare con moto rettilineo uniforme. Il fisico all'interno osserva che i corpi si muovono di moto rettilineo uniforme, non accelerano e galleggiano a mezz'aria essendo in assenza di peso. Nella seconda fase vengono accesi i razzi dell'astronave, accelerandola verso l'alto con accelerazione a. Tutti i corpi all'interno del laboratorio, allora, nel sistema di riferimento del fisico verranno visti accelerare verso il basso con la stessa accelerazione. Nella terza fase l'astronave viene posta in un campo gravitazionale e lasciata andare in caduta libera. Come abbiamo visto per il principio di equivalenza tutti i corpi cadono con la stessa accelerazione, in particolare ciò vale anche per il fisico e gli oggetti che lo circondano. Gli oggetti pertanto cadranno insieme a lui, dandogli l'impressione di galleggiare a mezz'aria come in assenza di peso. Nella quarta ed ultima fase l'astronave viene tenuta ferma in un campo gravitazionale in cui l'accelerazione di gravità ha lo stesso valore a della seconda fase. Anche in questo momento lo scienziato osserverà tutti i corpi venire attirati verso il basso con accelerazione a. Risulta quindi evidente che il fisico all'interno del suo laboratorio non è in grado di distinguere la prima situazione dalla terza, come anche la seconda dalla quarta.
La conseguenza di questo esperimento è riassumibile dicendo che un campo gravitazionale è localmente equivalente ad un sistema di riferimento non inerziale. Bisogna aggiungere localmente perché il campo gravitazionale in punti molto lontani può accelerare i corpi lungo direzioni diverse. Viceversa possiamo dire che un sistema di riferimento inerziale è equivalente ad un sistema in caduta libera in un campo gravitazionale.
Curvatura dello spaziotempo dovuta al campo gravitazionale.
Se consideriamo un sistema di riferimento inerziale, un raggio di luce si propaga in linea retta con velocità c. Rispetto ad un riferimento accelerato però, tale raggio verrà visto compiere un percorso curvo. Siccome un moto accelerato corrisponde ad un campo gravitazionale possiamo dire che la luce in un campo gravitazionale non si propaga in linea retta.
Questo fatto apparentemente sembra una contraddizione con la teoria di Maxwell, secondo la quale la luce dovrebbe seguire sempre percorsi rettilinei. Chi ci assicura però che una "retta" nello spazio fisico coincida con la retta della geometria euclidea?
Un segmento di una retta è il più breve cammino tra due punti. Nel caso di una superficie sferica, il cammino più breve che unisce due punti, ovvero il corrispondente di una retta, risulta essere un arco di cerchio massimo. Potremmo quindi pensare che la presenza di un campo gravitazionale incurvi lo spaziotempo a quattro dimensioni. La luce allora, pur continuando a seguire il percorso più breve tra due punti, non compierà più un cammino rigorosamente rettilineo.
Cerchiamo di vedere come un campo gravitazionale modifichi lo spaziotempo.
Rallentamento del tempo:
Consideriamo la seguente situazione:

Per un osservatore
inerziale O, esterno alla piattaforma rotante un orologio posto a distanza R
dal centro si muove con velocità v = w R e pertanto il suo ritmo risulterà
rallentato di un fattore ![]() rispetto all'orologio
di O (secondo le conclusioni della relatività ristretta). Soltanto l'orologio
posto al centro, che risulta in quiete rispetto a O, avanzerà con il suo stesso
ritmo.
rispetto all'orologio
di O (secondo le conclusioni della relatività ristretta). Soltanto l'orologio
posto al centro, che risulta in quiete rispetto a O, avanzerà con il suo stesso
ritmo.
Consideriamo ora un osservatore O' posto al centro della piattaforma. Egli vedrà gli altri orologi della piattaforma andare più lentamente del suo, nonostante questi siano in quiete rispetto al lui. La causa di questo ritardo è da ricercare nell'accelerazione centripeta a cui sono sottoposti tutti gli altri orologi della piattaforma. Siccome un moto accelerato è equivalente ad un campo gravitazionale possiamo concludere che il campo gravitazionale rallenta gli orologi.
Curvatura dello spazio:
Consideriamo ora un
sistema di riferimento inerziale K ed un sistema di riferimento K' non
inerziale in rotazione uniforme rispetto a K. Consideriamo anche una
circonferenza solidale con K:

Rispetto a K il rapporto fra la circonferenza in quiete ed il suo diametro è
π. Rispetto a K' che ruota in senso antiorario la circonferenza viene
vista ruotare in senso orario. Ogni piccolo segmento della circonferenza
viene visto da K' muoversi con una certa velocità v. In un certo istante ogni piccolo
segmento di cui è formata la circonferenza viene visto contrarsi rispetto a K'
secondo la legge della contrazione di Lorentz per cui il rapporto fra
circonferenza e diametro è, rispetto a K', diverso da π (il diametro non
subisce la contrazione di Lorentz perché non si muove rispetto a K' nel
senso della sua lunghezza). Con questo semplice esempio si dimostra che lo
spazio rispetto ad un sistema di riferimento accelerato non è piatto ma è
curvo, in quanto non valgono più le regole della geometria
euclidea. Poiché un campo gravitazionale è equivalente ad un sistema di riferimento
accelerato, lo spazio viene incurvato da un campo gravitazionale.
In realtà gli effetti di rallentamento del tempo e curvatura dello spazio sono due aspetti di un unico fenomeno fisico: la curvatura dello spaziotempo dovuta al campo gravitazionale.
Coordinate gaussiane e completa equivalenza di tutti i sistemi di riferimento.
Un generico spazio curvo ha una proprietà molto importante che lo raccorda, per così dire, al più familiare spazio piatto euclideo. Per quanto esso possa essere incurvato, è sempre possibile considerarne una porzione nella quale esso sia praticamente piatto. In ogni spazio-tempo curvo è dunque sempre possibile scegliere un sistema di coordinate curvilinee rispetto alle quali lo spazio-tempo è localmente piatto ed inerziale. Sottolineiamo che questa proprietà vale solo localmente, ovvero in una zona dove il campo gravitazionale si possa considerare costante nello spazio e nel tempo.
Gauss scoprì che per studiare le proprietà di una varietà n-dimensionale è sufficiente definire un sistema di coordinate curvilinee e riferirsi ad esse. Non occorre quindi dover osservare la varietà "da fuori", come immersa in uno spazio euclideo a dimensioni maggiori. Il problema è che per descrivere le proprietà di una varietà non euclidea dall'interno occorre una matematica piuttosto complessa. Questo però è l'unico modo per descrivere la struttura spaziotemporale in cui siamo immersi. Per studiare una superficie curva bidimensionale si possono usare dunque delle coordinate gaussiane. La distanza tra due punti nello spazio curvo può venire espressa per mezzo di un teorema di "Pitagora generalizzato", in cui compaiono i quadrati e i prodotti misti delle coordinate preceduti da particolari coefficienti, detti coefficienti metrici, il cui valore varia da punto a punto.
Per esempio nel caso di una superficie bidimensionale, dette x1 e x2 le coordinate gaussiane, la distanza tra due punti è data da: Dl2 = g11 Dx12 + g12 Dx1Dx2 + g22 Dx22.
I coefficienti metrici possono variare a seconda del sistema di riferimento gaussiano scelto, ma contengono tutte le informazioni sulla geometria della varietà che si sta studiando. Attraverso tali coefficienti, in particolare, è possibile descrivere le geodetiche della varietà.
Una volta noti i coefficienti metrici dello spaziotempo, è possibile dunque calcolare le sue geodetiche, ovvero le traiettorie che seguiranno i corpi in esso immersi (essi, infatti, quando sono in caduta libera si muovono attraverso lo spaziotempo come la luce, seguendo i percorsi che minimizzano il cammino da seguire). Come abbiamo visto un campo gravitazionale, e quindi la presenza di masse, modifica lo spaziotempo. Sono le equazioni di campo di Einstein che mettono in relazione la distribuzione di massa ed energia con i coefficienti metrici dello spaziotempo, determinando così anche le traiettorie dei corpi presenti.
Se fissata la distribuzione della massa-energia passiamo da un sistema di coordinate ad un altro, anche i coefficienti metrici cambiano. Le equazioni che descrivono il moto però restano invariate, in quanto la curvatura dello spaziotempo, che determina l'andamento dei fenomeni, è indipendente dal sistema di coordinate scelto. Possiamo dunque concludere che tutti i sistemi di riferimento, comunque accelerati sono equivalenti per la descrizione e spiegazione di tutti i fenomeni. La definizione di sistema inerziale allora non è più necessaria.
Redshift gravitazionale.
Abbiamo visto che la luce subisce l'influenza di un campo gravitazionale. Vediamo ora in particolare cosa succede ad un raggio luminoso che risale un campo gravitazionale.
Consideriamo un esperimento mentale ideato da Einstein:
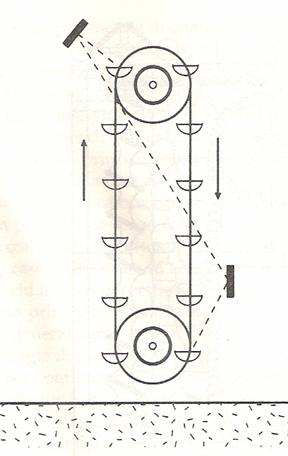 Si tratta di un nastro trasportatore con diverse coppe posizionate a
intervalli regolari. All'interno di ogni coppa è posto un singolo atomo. Quelli
nelle coppe di destra si trovano nello stato eccitato, quelli nelle coppe di sinistra
no. Dalla relatività ristretta si sa che E = m c2. Pertanto gli
atomi eccitati posti a destra pesano leggermente di più e fanno muovere la
macchina. Una volta arrivati in basso si potrebbe pensare di usare un
dispositivo per diseccitare gli atomi. Il fotone così emesso potrebbe viaggiare
verso l'alto per andare ad eccitare un altro atomo. In questo modo si potrebbe
realizzare il moto perpetuo. Siccome tale evento è reso impossibile dalle leggi
della termodinamica, qualcosa deve far sì che i fotoni vengano indeboliti
durante il loro spostamento. In questo modo parte dell'energia andrebbe persa,
gli atomi eccitati avrebbero un peso minore e il nastro trasportatore sarebbe
destinato a fermarsi. L'unica cosa che può indebolire il fotone è appunto il
campo gravitazionale. Come tutti i corpi, anche la luce perde energia
nell'opporsi alla forza di gravità. Questo fatto si concretizza con la
diminuzione della frequenza del raggio luminoso e va sotto il nome di Redshift
gravitazionale.
Si tratta di un nastro trasportatore con diverse coppe posizionate a
intervalli regolari. All'interno di ogni coppa è posto un singolo atomo. Quelli
nelle coppe di destra si trovano nello stato eccitato, quelli nelle coppe di sinistra
no. Dalla relatività ristretta si sa che E = m c2. Pertanto gli
atomi eccitati posti a destra pesano leggermente di più e fanno muovere la
macchina. Una volta arrivati in basso si potrebbe pensare di usare un
dispositivo per diseccitare gli atomi. Il fotone così emesso potrebbe viaggiare
verso l'alto per andare ad eccitare un altro atomo. In questo modo si potrebbe
realizzare il moto perpetuo. Siccome tale evento è reso impossibile dalle leggi
della termodinamica, qualcosa deve far sì che i fotoni vengano indeboliti
durante il loro spostamento. In questo modo parte dell'energia andrebbe persa,
gli atomi eccitati avrebbero un peso minore e il nastro trasportatore sarebbe
destinato a fermarsi. L'unica cosa che può indebolire il fotone è appunto il
campo gravitazionale. Come tutti i corpi, anche la luce perde energia
nell'opporsi alla forza di gravità. Questo fatto si concretizza con la
diminuzione della frequenza del raggio luminoso e va sotto il nome di Redshift
gravitazionale.
La frequenza di un'onda rappresenta il numero di cicli completi nell'unità di tempo. Dire che la luce arriva in alto con frequenza minore equivale perciò a dire che il tempo in basso scorre più lentamente che in alto. Tale variazione è molto piccola sulla Terra. Per fare un esempio in un'ora di tempo un orologio al suolo perderebbe soltanto un nanosecondo rispetto ad uno nello spazio. Gli effetti di questo fenomeno però si riveleranno molto più influenti in determinate circostanze come vedremo più avanti.
Epistemologia Popperiana ed esperimenti di corroborazione della Relatività Generale.
Oltre ad aver rivoluzionato il modo di concepire l'universo, la teoria della relatività di Einstein ha influenzato moltissimo anche l'epistemologia di Karl Raimund Popper, filosofo del XX secolo. Egli ha criticato il luogo comune secondo il quale una teoria risulta scientifica nella misura in cui può essere verificata dall'esperienza. In realtà il verificazionismo è un'utopia in quanto per aver verificato completamente una teoria dovremmo aver presenti tutti i casi, cosa evidentemente impossibile. Da una teoria discendono un'infinità di conseguenze, mentre i controlli effettivi che possono essere eseguiti sono in numero finito. Per definire la scientificità di una teoria è necessario rifarsi allora al criterio di falsificabilità. Secondo questo principio una teoria è scientifica nella misura in cui, in linea di principio, potrebbe essere smentita dall'esperienza. Affinché una teoria possa dirsi scientifica, dunque, devono poter essere concepiti esperimenti che potrebbero dare esiti contrastanti con quanto previsto dalla teoria stessa. La scienza così non è più il mondo delle verità certe, ma l'universo delle ipotesi che per il momento non sono ancora state falsificate. Quando una teoria scientifica ha superato il confronto con un'esperienza potenzialmente falsificante risulta corroborata. La corroborazione pur non essendo indice di verità, potrà fungere da criterio di scelta tra ipotesi rivali.
Vediamo quindi gli
esperimenti potenzialmente falsificanti che sono stati eseguiti per controllare
Tale deviazione è stata osservata fotografando la zona di cielo circostante il sole durante un'eclisse e la stessa zona di notte, in un diverso periodo dell'anno. Il confronto tra le due fotografie mostra una leggerissima differenza nella posizione apparente delle stelle, che nella foto scattata durante l'eclisse appaiono leggermente più lontane di quanto potremmo aspettarci se il cammino della luce fosse rettilineo. Secondo la teoria di Einstein la deviazione dovrebbe essere di 1, 74 secondi d'arco.
La seguente tabella riporta i valori ottenuti dalle misure sperimentali:
|
Data |
Località |
Spedizione |
Valore medio (sec. D'arco) |
|
|
Guinea |
Osservatorio di Greenwich (F. Dysone) |
|
|
|
Brasile |
Osservatorio di Greenwich |
|
|
|
Australia |
G.F. Dodwell |
|
|
|
Giappone |
Osservatorio di Tokio |
|
|
|
Brasile |
Soc. Geogr. Americ. |
|
|
|
Sudan |
Soc. Geogr. Americ. |
|
Come si può vedere, le osservazioni degli astronomi confermano che un raggio di luce viene deviato in un campo gravitazionale ed il valore ottenuto risulta in discreto accordo con quello previsto dalla teoria di Einstein.
Per campi
gravitazionali abbastanza deboli, infatti, le traiettorie dei pianeti
coincidono con le ellissi previste dalle equazioni Newtoniane. Se il campo è
più intenso, invece, si dovrebbe assistere ad una lenta precessione del
perielio. In altre parole l'asse maggiore dell'ellisse dovrebbe ruotare molto
lentamente nella direzione di rotazione del pianeta. Questo fenomeno è
osservabile nell'orbita di Mercurio. Secondo la teoria classica tale moto "a
rosetta", come viene definito, era dovuto alla presenza degli altri pianeti. Le
previsioni fatte con questo modello, o usando
Le misurazioni effettuate sul compagno di Sirio, una stella abbastanza vicina a noi, che genera un campo molto intenso avendo massa vicina a quella del Sole, ma un raggio doppio di quello terrestre, hanno confermato le previsioni della teoria.
La compagna di Sirio, nota come Sirio B, deve essere molto densa. Essa contiene infatti il 98% della massa del Sole avendo un raggio pari solo al doppio di quello terrestre. Questa stella non è una stella normale, ma una nana bianca.
 |
| Appunti su: rallentamento orologi sistemi accelerati, rallentamento del tempo moto accelerato relativitc3a0 generale, |
|
| Appunti Chimica |  |
| Tesine Biologia |  |
| Lezioni Geografia |  |