 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2410 | Gradito: |
Leggi anche appunti:I muoni μI muoni μ La Terra è continuamente bombardata da sciami di particelle Tesina opposizione tra materialismo e spiritualismoTesina Premessa: i punti in seguito esposti sono teorie, considerazioni Galileo galileiGALILEO GALILEI Nato a Pisa il 15 febbraio 1564 da Vincenzo Galilei, noto |
 |
 |
LE FORZE DI ATTRITO
ATTRITO RADENTE. Quando un corpo "striscia" sopra una superficie senza rotolare, il suo moto è ostacolato da una forza detta attrito radente e dovuta all'interazione tra superficie del corpo e "pavimento".
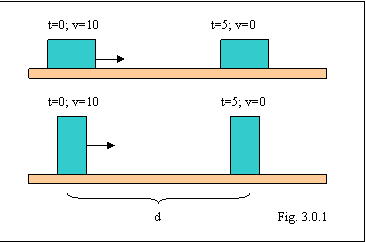
Questa forza può ben essere messa in evidenza con un semplice esperimento (Fig. 3.0.1):
una cassa viene lanciata con una velocità iniziale vi = 10 m/s e si osserva il tempo che impiega a fermarsi (5 secondi). L'esperimento è fatto in due modi: una prima volta il contatto con il pavimento avviene tramite la superficie laterale della cassa (grande superficie); in un secondo esperimento a strisciare è la base (piccola superficie). In entrambi gli esperimenti la cassa impiega 5 secondi a fermarsi e percorre lo stesso tratto d. Come interpretiamo questo esperimento?
Poiché nel tempo Dt = 5 secondi la velocità è passata da 10 m/s a zero, vuole dire che abbiamo un Dv = -10 m/s ed una corrispondente decelerazione
a = Dv/Dt = -10/5 = -2 m/s2
Ma dal paragrafo 2.0 noi sappiamo che le accelerazioni (e le decelerazioni che altro non sono se non accelerazioni negative) sono sempre da associare a forze:
chiamiamo forza di attrito radente quella che fa rallentare un corpo che striscia sopra una superficie (quando non ci siano altre evidenti forze "rallentatrici"!).
Una prima caratteristica delle forze di attrito è dunque quella di essere sempre dirette in modo opposto alla velocità dell'oggetto e di "sparire" non appena l'oggetto si fermi.
Una seconda caratteristica deducibile dall'esperimento sopra descritto è che le forze di attrito non dipendono dalla quantità di superficie in contatto, nel senso che non cambiano se striscia una superficie grande o una piccola (dipendono però dai materiali di cui sono fatti "pavimento" e "oggetto strisciante").
Non pensate ai pattini da ghiaccio come controesempio a quanto appena detto: con quel tipo di pattini è infatti noto che una diminuzione della superficie in contatto provoca una diminuzione di attrito, e ciò è esattamente il contrario di quanto da noi appena sostenuto! I pattini su ghiaccio rappresentano però una caso un po' speciale, perché l'aumento di pressione (associato alla diminuzione di superficie dei pattini) provoca lo scioglimento momentaneo dello strato di ghiaccio a contatto con i pattini, per cui i questi non strisciano sul ghiaccio ma sono "sospesi" su un piccolissimo strato d'acqua, e questo riduce chiaramente moltissimo l'attrito. Provate però a muovervi con i pattini sul pavimento di casa: sicuramente: il pavimento non si scioglie e avere pattini con piccola o grande superficie non fa più differenza.
Una terza caratteristica è questa: la forza di attrito dipende dalla forza che preme il corpo contro la superficie.
Volendo tradurre tutto con una formula matematica, abbiamo
Far = Kar Peff
ove Kar
è una costante senza unità di misura che dipende dai materiali (oggetto
strisciante e pavimento) e Peff
è la forza che "effettivamente" preme l'oggetto strisciante contro il
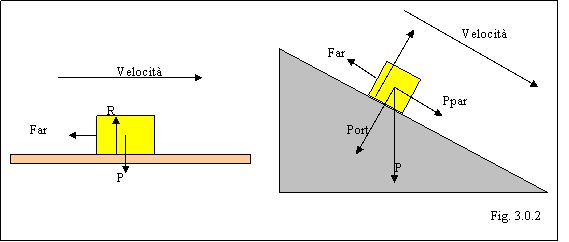
pavimento. Facciamo qualche altra precisazione circa questa "forza effettiva"
(fig.3.0.2):
se l'oggetto che striscia è posto sopra un piano orizzontale è chiaro che chi preme è l'intero peso dell'oggetto (Peff = P);
se invece l'oggetto striscia sopra un piano inclinato è chiaro che a premere contro il piano non è tanto P quanto la sua componente ortogonale Port (Peff = Port);
se l'oggetto viene fatto strisciare su un piano orizzontale da una forza che ha anche una componente verticale verso l'alto, Peff è dato dalla differenza tra il peso del corpo e la componente verticale della forza trainante (vedi problema 53 pag. 142 del libro di testo).
ESEMPIO. Un corpo con massa 300 Kg striscia su un piano inclinato (60°) con coefficiente di attrito radente pari a 0,4. Determinare la forza di attrito radente che si oppone al moto e la forza Ppar che è causa del moto.
P 3000 N
Ppar sin(60°) = 3000 0,86 = 2600 N
Port cos(60°) = 3000 0,5 = 1500 N
Far Peff 1500 = 600 N
Abbiamo dunque una forza di 2600 N che spinge verso il fondo del piano inclinato ed una forza di 600 N che si oppone a questo moto (spinge verso la cima del piano inclinato).
ESEMPIO. Un corpo di 100 Kg è posto su un piano inclinato (45°) e scende a velocità costante. Determinare il coefficiente di attrito radente.
Riferiamoci alla figura 3.0.2. Se la velocità è costante allora le forze agenti sul blocco devono annullarsi; ortogonalmente al piano abbiamo Port e la reazione vincolare R che già si annullano, lungo il piano abbiamo Ppar e Far: visto che il blocco scende al velocità costante dovrà essere Ppar = Far.
P 1000 N
Ppar sin(45°) = 1000 0,7 = 700 N
Port cos(45°) = 1000 0,7 = 700 N
Per il piano inclinato sappiamo che la forza che preme è Port; avremo dunque
Far = K
Poiché in questo caso la forza di attrito è uguale a Ppar avremo
700 N = K 700 N T K = 1.
NOTA BENE: quando con la nostra auto procediamo su una strada piana alla velocità di 100 Km/h, il motore fornisce una forza "in avanti" e, nonostante questa forza, l'auto non accelera. Perché? Se non accelera è perché, oltre alla forza "in avanti" del motore, c'è una forza "all'indietro" - dovuta all'attrito dell'auto con l'aria - esattamente contraria a quella del motore. Se non esistesse l'attrito, una volta raggiunta la velocità prescelta, potremmo spegnere il motore ed andare avanti all'infinito (le forze servono infatti solo per accelerare, non per i moti rettilinei uniformi). Eppure l'attrito è anche essenziale per la vita di ogni giorno: senza attrito sarebbe davvero difficile raccogliere un fazzoletto, tutto scivolerebbe inevitabilmente dalle nostre mani, camminare sarebbe impossibile.
ATTRITO VOLVENTE. Quando un corpo, invece di strisciare, rotola sopra una superficie esiste una forza che si oppone al moto detta forza di attrito volvente. Questa forza dipende dal "peso effettivo" del corpo ed anche dal raggio:
Fav = Kav Peff/r (3.0.2)
ove Kav è il coefficiente di attrito volvente ed r il raggio.
Kav ha come unità di misura il metro.
(3.0.2) ci dice che la forza di attrito volvente aumenta se aumenta il "peso efficace" Peff (direttamente proporzionale a Peff) e se diminuisce il raggio r (inversamente proporzionale a r).
In generale l'attrito volvente è molto minore dell'attrito radente (meglio rotolare che strisciare; l'invenzione della ruota è considerata una pietra miliare della civiltà) e le ruote alte contribuiscono a diminuire l'attrito volvente.
 |
| Appunti su: https:wwwappuntimaniacomscientifichefisicale-forze-di-attrito93php, |
|
| Appunti Biologia |  |
| Tesine Chimica |  |
| Lezioni Geografia |  |