 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3710 | Gradito: |
Leggi anche appunti:Il lavoro, l' energia cinetica e l'energia potenzialeIL LAVORO , L' ENERGIA CINETICA E L'ENERGIA POTENZIALE La massaLA MASSA Che cos'è la massa? Possiamo avere due definizioni Newton: la teoria corpuscolare della luceNEWTON: LA TEORIA CORPUSCOLARE DELLA LUCE Le leggi della riflessione e della |
 |
 |
Le equazioni di Maxwell
1 Il teorema di Gauss per il campo elettrico e la circuitazione
Per introdurre le quattro principali equazioni è necessario un riferimento al teorema di Gauss per i campo elettrico e al concetto di "circuitazione".
Teorema di Gauss:
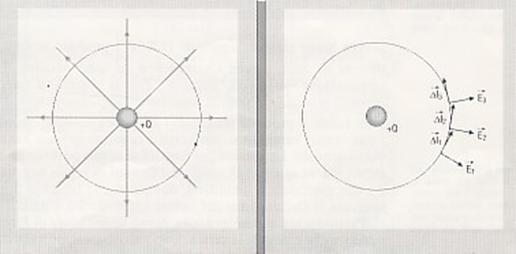
Determiniamo il flusso del campo elettrico, generato da una carica puntiforme Q, attraverso una superficie sferica di raggio r, avente il centro coincidente con la carica.
Il risultato che ha valore generale per qualunque distribuzione di carica e qualunque superficie, lo si ottiene con un calcolo abbastanza semplice.
 Una sfera circonda una carica
elettrica +Q
Una sfera circonda una carica
elettrica +Q
Per calcolare il flusso del
campo ![]() attraverso la
superficie, suddividiamo quest'ultima in tante superfici
attraverso la
superficie, suddividiamo quest'ultima in tante superfici
Il campo elettrico della carica puntiforme
posta al centro della sfera ha la stessa intensità E in tutti i punti di S
(superficie), la direzione del campo varia da punto a punto. Suddividiamo la
superficie in parti ![]() di area uguale e abbastanza piccole da poterle considerare
piane.
di area uguale e abbastanza piccole da poterle considerare
piane.
Il flusso ![]() attraverso ogni piccola superficie
attraverso ogni piccola superficie ![]() risulta uguale a
risulta uguale a
![]() =
= ![]()
![]() = E
= E![]()
Il flusso di ![]() attraverso tutta la
superficie sferica è la somma dei flussi parziali attraverso ciascuna piccola
superficie
attraverso tutta la
superficie sferica è la somma dei flussi parziali attraverso ciascuna piccola
superficie ![]() :
:
![]() =
= ![]() 1
1![]() +
+![]() 2
2![]() 2+
2+![]() 3
3![]() 3+.=
3+.= ![]()
Il flusso è uguale al prodotto dell'intensità E del campo per la somma delle aree delle piccole superfici, che è uguale all'area della superficie S della sfera:
![]() = ES
= ES
dato che E = Ke ![]() e S = 4
e S = 4![]() r2
otteniamo:
r2
otteniamo:
![]() = 4
= 4![]() KeQ
KeQ
Il flusso attraverso la sfera è proporzionale alla carica Q che essa contiene e non dipende dal raggio della sfera. Infatti, se svolgiamo lo stesso calcolo considerando una sfera di raggio 2r, il risultato non cambia perché si compensano la diminuzione dell'intensità del campo elettrico, inversamente proporzionale al quadrato del raggio r, con l'aumento dell'area della superficie della sfera, direttamente proporzionale al quadrato di r. Si nota che il flusso dipende solo dalla carica contenuta nella superficie, ha segno positivo per una carica positiva e negativo per una carica negativa.[1]
Con il teorema di Gauss, che vale non solo per i campi elettrostatici ma anche per i campi elettrici che variano con il tempo, abbiamo enunciato la prima delle equazioni di Maxwell.
In generale è possibile enunciare il teorema di Gauss valido per il magnetismo: il flusso di un campo magnetico attraverso qualsiasi superficie chiusa è uguale a zero.
Ecco una prima diversità tra
il campo elettrico e il campo magnetico. Mentre il flusso di ![]() è proporzionale alla
quantità di carica racchiusa nella superficie, il flusso di
è proporzionale alla
quantità di carica racchiusa nella superficie, il flusso di ![]() è sempre uguale a
zero. Ciò riflette una profonda diversità tra le sorgenti di campo elettrico e
di quello magnetico. Mentre vi sono cariche elettriche positive e cariche
elettriche negative, non esiste un analogo magnetico. Non vi sono infatti poli
magnetici liberi.
è sempre uguale a
zero. Ciò riflette una profonda diversità tra le sorgenti di campo elettrico e
di quello magnetico. Mentre vi sono cariche elettriche positive e cariche
elettriche negative, non esiste un analogo magnetico. Non vi sono infatti poli
magnetici liberi.
Il teorema di Gauss per il magnetismo vale sia per i campi statici che per quelli variabili nel tempo e rappresenta la seconda equazione di Maxwell.
La circuitazione
Le proprietà del campo
elettrico ![]() non sono espresse dal
teorema di Gauss; occorre infatti determinare la circuitazione.
non sono espresse dal
teorema di Gauss; occorre infatti determinare la circuitazione.
La circuitazione esprime una proprietà importante delle linee di un campo vettoriale.
Consideriamo una linea chiusa immersa in un campo descritto da un vettore, per esempio il campo elettrico.
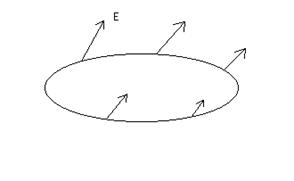
In questo caso la circuitazione del vettore lungo la linea chiusa viene determinata con il prodotto dell'intensità del vettore per la lunghezza della linea stessa.
Calcoliamo la circuitazione ![]()
![]() ) del campo elettrico di una carica puntiforme Q lungo una circonferenza che ha il
centro coincidente con la carica.
) del campo elettrico di una carica puntiforme Q lungo una circonferenza che ha il
centro coincidente con la carica.
 La circonferenza è concentrica alla carica +Q
La circonferenza è concentrica alla carica +Q
Per calcolare la
circuitazione del campo elettrico della carica lungo la circonferenza, essa
viene suddivisa in tanti spostamenti ![]()
La circuitazione risulta una somma di prodotti scalari
![]()
![]() ) =
) = ![]() 1
1![]() 1+
1+![]() 2
2![]() 2+. =
2+. = ![]()
calcolata lungo una serie di
intervalli di lunghezza ![]() nei quali pensiamo di
suddividere la circonferenza. Ciascuno di questi tratti è un segmento parallelo
alla tangente alla circonferenza e quindi è sempre perpendicolare al campo
elettrico, la cui direzione coincide con quella del raggio della circonferenza,
il prodotto scalare di vettori perpendicolari è nullo, la circuirazione sarà
quindi uguale alla somma di addendi nulli e quindi
nei quali pensiamo di
suddividere la circonferenza. Ciascuno di questi tratti è un segmento parallelo
alla tangente alla circonferenza e quindi è sempre perpendicolare al campo
elettrico, la cui direzione coincide con quella del raggio della circonferenza,
il prodotto scalare di vettori perpendicolari è nullo, la circuirazione sarà
quindi uguale alla somma di addendi nulli e quindi ![]()
![]() ) = 0 . Questo risultato vale per tutte le circonferenze
con il centro sulla carica, qualunque sia il loro raggio.
) = 0 . Questo risultato vale per tutte le circonferenze
con il centro sulla carica, qualunque sia il loro raggio.
È possibile concludere che la cicuitazione di un campo elettrostatico lungo un qualsiasi percorso chiuso è sempre nulla.
Tale conclusione introduce la terza equazione di Maxwell nel caso statico, l'equazione non vale più nel caso dinamico, cioè quando il campo elettrico varia nel tempo.
Dalla legge di
Faraday-Neumann sappiamo che la forza elettromotrice indotta ![]() è proporzionale alla
rapidità con cui varia il flusso
è proporzionale alla
rapidità con cui varia il flusso ![]() del campo magnetico
del campo magnetico ![]() attraverso una
ipotetica spira. Sugli elettroni che costituiscono la corrente indotta agisce
una forza esterna provocata dalla variazione di flusso del campo magnetico. Il
lavoro per unità di carica di questa forza esterna è per definizione la forza
elettromotrice indotta. Approssimiamo la spira con una serie di segmenti
attraverso una
ipotetica spira. Sugli elettroni che costituiscono la corrente indotta agisce
una forza esterna provocata dalla variazione di flusso del campo magnetico. Il
lavoro per unità di carica di questa forza esterna è per definizione la forza
elettromotrice indotta. Approssimiamo la spira con una serie di segmenti ![]() tangenti ad essa ed eseguiamo per ogni segmento il prodotto
scalare
tangenti ad essa ed eseguiamo per ogni segmento il prodotto
scalare ![]() , otteniamo così
, otteniamo così
![]() =
= ![]()
![]() , ricordando poi che
, ricordando poi che ![]() =
= ![]() , risulta
, risulta ![]() =
= ![]()
![]()
![]() e quindi
e quindi ![]() =
= ![]()
![]() )
)
Possiamo allora completare l'equazione di Maxwell che esprime la circuitazione del campo elettrico estendendola al caso dinamico:
![]()
![]() )= -
)= - 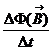
Volendo determinare la
circuitazione ![]() nel campo
nel campo ![]() , consideriamo il caso di un filo rettilineo percorso da una
corrente i. Per sfruttare la
simmetria del campo calcoliamo la circuitazione lungo una circonferenza di
raggio r con il centro sul filo e
disposta sul piano perpendicolare a esso, in ogni punto della circonferenza che
si considera, il campo e la tangente alla curva sono paralleli. Il campo
, consideriamo il caso di un filo rettilineo percorso da una
corrente i. Per sfruttare la
simmetria del campo calcoliamo la circuitazione lungo una circonferenza di
raggio r con il centro sul filo e
disposta sul piano perpendicolare a esso, in ogni punto della circonferenza che
si considera, il campo e la tangente alla curva sono paralleli. Il campo ![]() ha la stessa intensità
in tutti i punti della circonferenza, la circuitazione sarà uguale a
ha la stessa intensità
in tutti i punti della circonferenza, la circuitazione sarà uguale a
![]() = B
= B![]() Km
Km![]()
![]()
![]() =
= ![]() Kmi
Kmi
Anche in questo caso la circuitazione del campo prodotto dal filo non dipende dal raggio della circonferenza.
Tale risultato porta ad enunciare il noto teorema di Ampère: la circuitazione di un generico campo magnetico è proporzionale alla somma algebrica delle correnti concatenate[2].
![]() (
(![]() ) =
) = ![]() Km
Km![]()
Il teorema di Ampère rappresenta la quarta equazione di Maxwell nel caso statico (non dipendente da t).
2 Le quattro equazioni fondamentali ed il "termine mancante"
Le principali equazioni possono essere così schematizzate
![]() = 4
= 4![]() KeQ
KeQ
![]() 0
0
![]()
![]() )= -
)= - 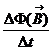
![]() (
(![]() ) =
) = ![]() Kmi
Kmi
Osservando le equazioni da
un punto di vista matematico Maxwell scorse due asimmetrie tra i campi ![]() e
e ![]() . La prima riguarda, da una parte, la presenza della carica Q nella legge di Gauss per il campo
elettrico e l'assenza di una carica analoga nella legge di Gauss per il campo
magnetico, dall'altra la presenza della corrente elettrica nella legge di
Ampère e l'assenza di una corrente "magnetica" nella legge di Faraday-Neumann.
Questa asimmetria si spiega con il fatto che non sono stati scoperti poli
magnetici isolati.
. La prima riguarda, da una parte, la presenza della carica Q nella legge di Gauss per il campo
elettrico e l'assenza di una carica analoga nella legge di Gauss per il campo
magnetico, dall'altra la presenza della corrente elettrica nella legge di
Ampère e l'assenza di una corrente "magnetica" nella legge di Faraday-Neumann.
Questa asimmetria si spiega con il fatto che non sono stati scoperti poli
magnetici isolati.
Vi è anche un'altra
importante asimmetria tra i due campi. Manca nella legge di Ampère un termine
analogo a quello che compare al secondo membro della legge di Faraday- Neumann,
cioè un termine proporzionale alla rapidità con cui varia il flusso del campo
elettrico: 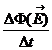
Partendo quindi da considerazioni di simmetria, Maxwell aggiunge questo "termine mancante" che gli consente di risolvere alcune ambiguità teoriche emerse nell'ambito delle quattro equazioni esposte.
Il processo che consente a Maxwell di trovare tale termine viene qui riportato.
Consideriamo il processo di carica di un condensatore[3]. Mentre le armature si caricano, nei fili circola una corrente di intensità sempre più piccola che genera nello spazio un campo magnetico. Le linee di campo circondano i fili e non dovrebbero esistere attorno al condensatore.
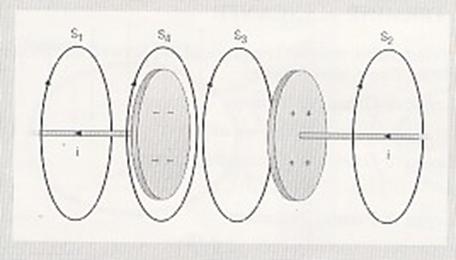
La corrente
i e il campo magnetico ![]() subiscono, attorno al condensatore, una discontinuità
difficile da interpretare.
subiscono, attorno al condensatore, una discontinuità
difficile da interpretare.
La circuitazione del campo
magnetico lungo le circonferenze S1 e S2 è uguale a ![]() Kmi e
dovrebbe essere nulla lungo S3. Il ragionamento porta a concludere
che lungo la circonferenza S4 la circuitazione diventa
improvvisamente uguale a zero.
Kmi e
dovrebbe essere nulla lungo S3. Il ragionamento porta a concludere
che lungo la circonferenza S4 la circuitazione diventa
improvvisamente uguale a zero.
Se alla legge di Ampère
viene aggiunto un termine proporzionale alla rapidità con cui varia il campo
elettrico, precisamente ![]()
![]()
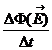 , l'ambiguità
sparisce.
, l'ambiguità
sparisce.
Questo termine venne interpretato da Maxwell come una corrente, la corrente di spostamento, la quale "prolunga" tra una armatura e l'altra la corrente che attraversa i conduttori.
Riscrivendo quindi la legge di Ampère con il nuovo termine otteniamo:
![]() (
(![]() ) =
) = ![]() Kmi+
Kmi+![]()
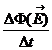 =
= ![]() Km
Km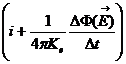
La corrente di spostamento is è pari a 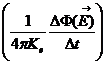 .
.
È possibile dimostrare che essa è pari alla corrente che circola nei conduttori.
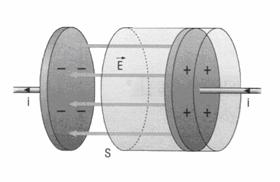
Il flusso del campo elettrico attraverso una superficie cilindrica che racchiude un'armatura del condensatore è pari al flusso calcolato nello spazio tra le armature.
![]()
per il teorema di Gauss vale
![]()
Dopo un intervallo di tempo ![]() , mentre procede il processo di carica, sull'armatura si
deposita una carica aggiuntiva
, mentre procede il processo di carica, sull'armatura si
deposita una carica aggiuntiva ![]() la quale aumenta di
la quale aumenta di ![]() il campo elettrico e
di
il campo elettrico e
di ![]() il flusso:
il flusso:
![]() =
= ![]() S
S
Analogamente, per il teorema
di Gauss ![]() S =
S = ![]() ,
,
dividiamo quindi ambo i
membri per ![]() ottenendo
ottenendo ![]()
![]() risulta come la
corrente i che circola nel
conduttore, di conseguenza
risulta come la
corrente i che circola nel
conduttore, di conseguenza
![]()
ricordando poi che ![]() =
= ![]() S, ricaviamo i
S, ricaviamo i
i = 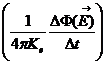
il valore della corrente di spostamento risulta così uguale a quello della corrente che circola nel conduttore.
 La corrente di spostamento is ha la stessa intensità della
corrente di conduzione nei fili e genera un campo magnetico attorno al
condensatore.
La corrente di spostamento is ha la stessa intensità della
corrente di conduzione nei fili e genera un campo magnetico attorno al
condensatore.
L'aggiunta del termine alla legge di Ampère rende simmetrici i campi elettrico e magnetico per ciò che riguarda la loro variazione nel tempo. Un campo magnetico variabile genera un campo elettrico (legge Faraday-Neumann) e anche un campo elettrico variabile genera un campo magnetico (termine aggiunto da Maxwell).
È possibile ora presentare le equazioni di Maxwell nelle modalità più diffuse .La seguente forma, a prescindere dal mezzo considerato, distingue i casi statico e dinamico o generale.

Vengono di seguito rappresentate le equazioni, valide per un qualsiasi mezzo materiale, nella forma integrale e in quella differenziale. Per comprendere appieno il significato di tali scritture, sono necessari concetti di analisi vettoriale non contemplati dalla didattica liceale, pertanto, in questa sede ci si limita ad una schematica esposizione.
Forma integrale Forma differenziale
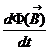
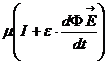
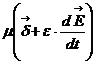
Corrente di spostamento Is =  densità di spostamento
densità di spostamento ![]() =
= 
Se si considerano i valori ![]() ( permeabilità magnetica del vuoto) e
( permeabilità magnetica del vuoto) e ![]() [4](
costante dielettrica assoluta del vuoto), nelle equazioni numero 4, la corrente
di conduzione e la densità diventano nulle e le stesse equazioni risultano
simmetriche alle numero 3.
[4](
costante dielettrica assoluta del vuoto), nelle equazioni numero 4, la corrente
di conduzione e la densità diventano nulle e le stesse equazioni risultano
simmetriche alle numero 3.
Le equazioni di Maxwell espresse in forma differenziale nel vuoto ( o nell' "etere"), essendo nulle le correnti di conduzione e le cariche elettriche, raggiungono una perfetta simmetria tra campo magnetico e campo elettrico.
Le conseguenze delle equazioni di Maxwell risultano estremamente importanti.
Un campo elettrico che varia rapidamente nel tempo genera un flusso anch'esso variabile e, per la quarta equazione, induce un campo magnetico. Allo stesso modo, un campo magnetico che varia rapidamente nel tempo genera un flusso variabile e quindi induce un campo elettrico (terza equazione).
Innescato quindi un campo che varia rapidamente nel tempo, si genera una catena senza fine di campi che continuano a produrre effetti di induzione reciproca e quindi si estendono nello spazio.
Si propaga allora un campo elettromagnetico: una nuova grandezza costituita da un campo elettrico e da un campo magnetico inestricabilmente legati tra loro.
Il segno del flusso dipende dal coseno dell'angolo fra i due vettori ![]() e
e ![]() : per una carica positiva essi hanno lo stesso verso mentre
per una carica negativa essi hanno versi opposti.
: per una carica positiva essi hanno lo stesso verso mentre
per una carica negativa essi hanno versi opposti.
 |
|
| Appunti Biologia |  |
| Tesine Chimica |  |
| Lezioni Geografia |  |