La teoria delle stringhe

LA TEORIA DELLE STRINGHE

1 INTRODUZIONE

Con la relatività einsteniana e la meccanica quantistica l'uomo ha fatto grandi progressi nella comprensione dell'universo fisico. Comunque sia, i fisici non troveranno pace finché non avranno svelato i misteri del cosmo fino al livello più profondo. E che queste due teorie non siano delle cosiddette TOE (theory of everything, teorie del tutto) è comprensibile, poiché i loro domini di applicazione sono opposti e, di solito, solo una delle due entra in gioco; se entrambe, per oggetti molto massivi e contemporaneamente molto piccoli (come la regione centrale di un buco nero o il Big Bang), lo fanno, cominciano i problemi. Capita che la probabilità quantomeccanica di un certo evento dia come risultato infinito.

A questo punto entra in gioco la teoria delle stringhe.

La musica è da sempre fonte di ispirazione per chi medita sulla natura: si pensi alla "musica delle sfere" dei pitagorici. La teoria delle stringhe porta la musica del cosmo dal piano metafisico a quello fisico: i costituenti elementari, per questa teoria, sono come piccole corde di violino che a seconda del loro modo di vibrare orchestrano la vita del cosmo.

Come primo acchito alla teoria, si nota che le particelle puntiformi vengono sostituite da una sorta di filamenti unidimensionali. Nel Modello Standard, fondato sulle particelle puntiformi, i risultati sono stati importanti, ma non prevedevano la gravità. È il 1984 l'anno in cui Michael Green e John Schwarz trovarono una prima prova convincente del funzionamento delle stringhe. Inoltre il fatto che le stringhe (da non confondere con una comune stringa che è perlomeno tridimensionale) siano unidimensionali è una radicale innovazione, che si ripercuote anche sullo spazio-tempo ma che non viola le leggi formulate fin qui su particelle puntiformi, poiché le stringhe sono molto piccole, in media della lunghezza di Planck, e con la nostra attuale tecnologia sembrano puntiformi.

1 BREVE STORIA DELLE STRINGHE

Nel 1968 il ventiseienne fiorentino Gabriele Veneziano, ricercatore al CERN (Conseil Européen pour la Recherche Nucléaire) di Ginevra, stava cercando di capire la forza nucleare forte, quando fece una sensazionale scoperta. Veneziano scoprì che una formula ormai vecchia di duecento anni creata dal matematico svizzero Eulero, la funzione beta di Eulero, si adattava perfettamente ai dati sull'interazione forte. Come una formula imparata a memoria da uno studente, nessuno si rendeva conto del perché la formula funzionasse.

Nel 1970 Yoichiro Nambu, Holger Bech Nielsen e Leonard Susskind presentarono una spiegazione fisica per la straordinaria precisione teorica della formula di Eulero. Rappresentando la forza nucleare attraverso vibranti stringhe ad una sola dimensione, questi fisici mostrarono come la funzione di Eulero descrivesse accuratamente queste forze. Ma anche dopo che i fisici ebbero capito la spiegazione fisica per l'intuizione di Veneziano, la descrizione che le stringhe davano della forza forte faceva predizioni che contraddicevano direttamente le esperienze. La comunità scientifica perse presto interesse nella teoria delle stringhe e il Modello Standard, con le sue particelle e i suoi campi, rimase a farla da padrone.

Tuttavia alcuni ricercatori continuarono ad occuparsene colpiti dall'eleganza della teoria. Come diceva Schwarz:

la struttura matematica della teoria era così elegante e aveva così tante proprietà miracolose, che doveva per forza indicare qualcosa di molto profondo.[1]

Uno dei problemi della teoria era la sua eccessiva ricchezza. Alcuni modi di vibrazione delle stringhe si addicevano ai gluoni, ma esistevano anche modelli di stringa con modelli di particelle aggiuntive che non avevano nulla a che fare con i risultati sperimentali.

Nel 1974 Schwarz e Joel Scherk mostrarono che queste particelle avevano le stesse proprietà che si ipotizzavano per i gravitoni. Schwarz e Scherk argomentarono che la teoria delle stringhe non aveva avuto successo perché i fisici ne avevano frainteso gli scopi. Ma le scoperte dei fisici delle stringhe furono ignorati dalla comunità scientifica, visti anche gli straordinari risultati che andava raggiungendo la cromodinamica quantistica in quegli anni.

La situazione non mutò fino al 1984. In quell'anno uscì un articolo di Schwarz e Green in cui si mostrava come tutte le quattro forze fondamentali potevano essere spiegate con la teoria delle stringhe e che il conflitto tra meccanica quantistica e relatività generale poteva essere risolto. Gli anni tra il 1984 e il 1986 sono stati battezzati il periodo della "prima rivoluzione delle superstringhe". Comparvero un gran numero di articoli che mostravano come molte parti, faticosamente scoperte dal Modello Standard, emergevano in modo naturale dalla teoria delle stringhe. Nonostante gli straordinari risultati raggiunti, il percorso delle stringhe fu difficoltoso, poiché mentre per la fisica teorica le equazioni difficili da risolvere portano a risoluzioni approssimate, per le stringhe è arduo formulare le equazioni, cosicché ci si trova ad avere soluzioni approssimate di equazioni approssimate. Come un tesoro chiuso in una cassaforte senza serratura, con un piccolo spiraglio, la terra promessa della teoria delle stringhe brillava irraggiungibile, senza una chiave per dischiuderla.

Durante il convegno "Strings 1995" alla University of Southern California, Edward Witten propose il passo successivo della teoria, la M-theory, dando il via alla "seconda rivoluzione delle superstringhe".

Attualmente la rivoluzione è in atto e nuove tecniche sembrano aggirare la precedenti difficoltà, ma risulta ancora molto difficile trovare una verifica sperimentale dell'esistenza delle stringhe per motivi di limitata tecnologia, che potrebbero essere risolti a breve con la costruzione dell'acceleratore LHC (Large Hadron Collider) presso il CERN.

2 IL RITORNO ALL'ATOMO DEI GRECI

Abbiamo detto che le stringhe sono il costituente fondamentale della materia, che si trovano alla lunghezza di Planck e quindi a una dimensione molto piccola per la nostra attuale tecnologia. Resta da capire di cosa sono fatte le stringhe: a tal proposito si possono trovare due possibilità.

La prima possibilità è che le stringhe siano davvero quelle che i greci chiamavano "atomi", cioè "indivisibili", come l'ultima scatola di una matrioska, il punto d'arrivo di tutte le strutture del mondo microscopico. Se così non fosse dovremmo abbandonare la ricerca delle stringhe verso qualcosa di ancora più piccolo e fondamentale. Una stringa è perciò la parte fondamentale della materia, non è fatta di niente.

La seconda possibilità deriva dal fatto che ancora non sono state trovate le stringhe e che non sappiamo se siano davvero i costituenti ultimi della materia. La storia insegna che ogni qualvolta miglioriamo le nostre tecniche, troviamo dei costituenti più piccoli che costituiscono un ulteriore livello di base. Come già detto non possiamo verificare tutto ciò fino a che non riusciremo a trovare una tecnologia in grado di arrivare a queste dimensioni.

Considerate le stringhe come i costituenti ultimi della materia, vediamo l'importanza delle stringhe nella ricerca. Nel Modello Standard, oltre a non includere la gravità, un altro difetto è dato dal fatto che non spiega come mai la natura abbia scelto una lista di particelle e forze nel modo che conosciamo, e come mai abbia dato a queste particelle determinati valori. Questi valori sono stati misurati e presi dai teorici per poterli usare nei propri calcoli. Il Modello Standard è molto flessibile, ragion per cui ogni cambiamento che potrebbe scaturire dagli esperimenti non altererebbe la funzionalità del modello, in cui questi dati sono in pratica input assegnati dai fisici.

La teoria delle stringhe, al contrario, non ha bisogno di input esterni e tutti i parametri sono sottoposti al suo potere esplicativo. Per capire questo si pensi ad un violino. Le diverse note che scaturiscono dallo strumento corrispondono a diversi modi di vibrazione delle corde. Le corde vibrano in un numero infinito di modi, detti risonanze, che sono tipi d'onda con un numero intero di picchi e ventri. Allo stesso modo le stringhe: diversi modi di vibrare di una stringa fondamentale danno origine a diverse masse e cariche di gauge (cioè quelle associate alle forze).

Pensiamo alle masse: la massa di una particella dipende, secondo la relatività, dall'energia e viceversa. L'energia dipende da ampiezza e lunghezza d'onda. Maggiore è la prima e minore è la seconda, maggiore sarà l'energia. Quindi, poiché a maggior energia corrisponde maggior massa, per corpi più pesanti la stringa oscilla più violentemente, per corpi più leggeri oscilla più dolcemente. Allo stesso modo, tutte le proprietà delle particelle fondamentali fin qui scoperte, fotoni, bosoni di gauge deboli e gluoni, oltre alle loro interazioni dipendono da modi di vibrazione delle stringhe. Non solo: la cosa fondamentale è che anche le proprietà della particella mediatrice della gravità sono spiegate in termini di vibrazione, il che ci assicura che anche la gravità è parte integrante delle stringhe.

Tutto questo causa anche un profondo cambiamento nel modo di vedere le cose: se prima per descrivere la differenza nella materia dicevamo "è fatta in modo diverso" e che il "qualcosa" che componeva l'elettrone aveva carica positiva, mentre il neutrino era fatto da "qualcosa" neutro, ora diciamo che tutta la materia è fatta allo stesso modo, ogni particella è fatta da un'unica stringa e tutte le stringhe sono assolutamente identiche, le differenze nascono da diversi modi di vibrazione:

quelle che sembrano particelle elementari di diverso tipo, non sono che varie "note" suonate da un solo tipo fondamentale di stringa. L'universo composto da un numero enorme di queste piccole corde vibranti, è una grande sinfonia cosmica.[2]

Poiché ogni evento o manifestazione del cosmo è descrivibile, a livello elementare, in termini di interazioni tra i suoi costituenti fondamentali, la teoria delle stringhe promette di essere un'unica, unitaria e onnicomprensiva descrizione dell'universo: una vera Teoria del Tutto.

Un simbolo del potere creativo del pensiero umano

Brian Greene (9 Febbraio 1963, New York) è un fisico tra i più famosi sostenitori della teoria delle stringhe. Dal 2003 è stato professore alla Columbia University. Fin da piccolo fu un prodigio in matematica e fu accompagnato da un professore universitario per fare degli studi di matematica più avanzati rispetto al livello della sua età. Nel 1980 Brian Greene entra ad Harvard con il suo grado di Bachelor. Va a Oxford University come studente Rhodes.

Nel 1999 pubblica in Italia con Einaudi L'universo elegante: supestringhe, dimensioni nascoste e la ricerca della teoria ultima. In questo libro spiega in modo semplice e geniale la teoria delle stringhe con l'intento di divulgare argomenti veramente molto complessi.

Nel 2000 riceve il premio Aventis (premio inglese per la saggistica scientifica) e arriva finalista al premio Pulitzer. Il secondo libro di Brian Greene esce nel 2004: La trama del cosmo (titolo inglese: The fabric of the Cosmos).

LA MUSICA DELLE STRINGHE

Abbiamo visto che massa e cariche delle particelle sono il risultato della vibrazione delle stringhe. Se riuscissimo a stabilire quali sono i modi di vibrazione permessi saremmo in grado di spiegare perché le particelle elementari hanno le proprietà sperimentalmente osservate. Dovremmo teoricamente pizzicare una stringa. Ovviamente questo è impossibile essendo così piccola. La matematica, però, ci permette di sentire teoricamente la musica delle stringhe. Tuttavia per ora, come già detto più volte, nonostante l'euforia causata dall'idea della creazione di una TOE, non siamo riusciti a verificare sperimentalmente tutte le scoperte teoriche.

La teoria trova, inoltre, vari ostacoli: uno di questi è la tensione.

Vi trovate di fronte a due corde, una tesissima e l'altra quasi per niente: ad esempio una corda di pianoforte ed un laccio di scarpe. Dovendo farle vibrare allo stesso modo, di sicuro trovereste molto più faticoso far oscillare la prima rispetto alla seconda poiché richiederebbe più energia. Analogamente allungando una molla l'energia potenziale aumenta.

Anche per le stringhe si nota che a parità di vibrazione l'energia aumenta all'aumentare della tensione e, poiché siamo a distanze veramente infinitesimali, bisogna seguire le regole della Meccanica Quantistica: è necessario quantizzare anche questa energia, proprio com'è accaduto circa un secolo prima con i pacchetti di Planck. L'energia minima, chiamata energia di Planck, con cui un stringa può contribuire alla massa della particella è proporzionale alla tensione.

E non stiamo parlando di valori qualsiasi: la tensione fondamentale di una stringa, chiamata ovviamente Tensione di Planck, è dell'ordine di 10¹⁹ masse protoniche.

Ma se ci fermassimo qui non prenderemmo in considerazione un elemento fondamentale del mondo microscopico: le fluttuazioni quantistiche. Infatti nell'ambito della teoria il contributi delle fluttuazioni alla massa delle particelle sarebbe negativo. In questo modo l'energia elevatissima della stringa viene controbilanciata dagli effetti quantistici: si annullano quasi completamente, dando origine a quelle che consideriamo particelle fondamentali. Per fare un esempio: si pensa che nel modo di vibrazione candidato a rappresentare il gravitone la cancellazione sia totale, di conseguenza la particella risultante non abbia massa, come era previsto dal fatto che la gravità si trasmette a velocità della luce e quindi per la relatività la particella responsabile dovrebbe avere, come per il fotone, massa nulla.

Come detto, le stringhe possono avere infiniti modi di vibrazione, e quelli che portano alla cancellazione totale sono pochi. Di conseguenza, risulta per la teoria che esistono infinite particelle fondamentali, anche pesantissime. Siccome i nostri acceleratori non vanno oltre le 1000 masse protoniche, siamo ben lontani da trovare queste presunte particelle. Comunque si può pensare al Big Bang come ad un esempio. Il Big Bang, con la sua straordinaria quantità di energia, dovrebbe aver prodotto molte di queste particelle a massa enorme. Tuttavia le grandi masse decadono velocemente, dando origine a una serie di masse più leggere. Se potessimo trovare, però, anche una sola di queste masse pesanti, avremmo una prova della validità della teoria.

4 LE STRINGHE LASCIANO IL SEGNO

Siamo abituati a pensare a traiettorie di particelle (word-line), linee sinuose che si sviluppano nello spazio-tempo. Per le stringhe le cose cambiano: immaginiamo una stringa come una formina per fare bolle di sapone. Muovendosi nello spazio-tempo lascerà dietro di sé una scia: un'elegante superficie bidimensionale, ottenuta affiancando le posizioni occupate nei diversi istanti. Tale superficie è il foglio d'universo (world-sheet) di una stringa (vd. figura accanto).

Sebbene in questo strano mondo sembrerebbero esistere stringhe in grado di attraversarsi come se nulla fosse, in generale due stringhe che si incontrano interagiscono. 

Le stringhe aperte 'scontrandosi' possono unire i propri estremi o incrociarsi, come nel crossing-over, scambiandosi frammenti reciprocamente. 

Stringhe chiuse possono invece fondersi in una nuova stringa, determinando un foglio d'universo topologicamente simile ad un cilindro con due estremità aperte. 

Tuttavia, come accade  successivamente ad  un processo di annichilazione, la nuova stringa potrebbe 'sdoppiarsi' nuovamente in due stringhe. Nel foglio d'universo sarebbero presenti ora quattro estremità aperte.

A loro volta le stringhe potrebbero reinteragire e la nuova stringa ridividersi, generando 'un buco' nel foglio e rendendolo topologicamente simile ad una ciambella.

Queste fusioni e sdoppiamenti potrebbero avvenire in diversi modi. Fortunatamente però nell'analisi delle interazioni non interessa tanto la geometria, quanto la topologia del foglio dell'universo descrivente il processo: non è importante cioè la precisa forma ma le proprietà, quali il numero di buchi presenti: il che semplifica la situazione! E questo non è l'unico risultato positivo.  Come si nota nei fogli d'universo, avendo le stringhe una propria estensione a differenza delle particelle elementari, le

Interazione fra particelle

interazioni non avvengono in un preciso punto dello spazio tempo. 

Tale inconveniente nelle teorie 'particellari' porta infatti all'origine di infiniti che spuntano nelle equazioni creando non pochi problemi e rendendole talvolta irrisolvibili. Ostacoli superati grazie agli appena 10^{-33 cm delle stringhe.}

5 DIMENSIONI CHE L'OCCHIO NON VEDE

Questa teoria non sembra però esser formulata per il nostro universo. Le stringhe infatti richiederebbero delle dimensioni extra in cui vibrare, oltre alle nostre 4 (3 spaziali + 1 temporale).

In verità, prima dell'avvento della teoria delle stringhe, le 4 dimensioni non sembravano accontentare proprio tutti, come il fisico polacco Kaluza, il quale pensò di riformulare la Relatività Generale in 5 dimensioni (4+1) ed il risultato fu sbalorditivo. Come conseguenza dell' introduzione di una dimensione spaziale in più spuntarono fuori spontaneamente dai suoi ragionamenti matematici le equazioni di Maxwell! Aggiungendo una nuova dimensione l'elettromagnetismo scaturiva dalla Relatività Generale come conseguenza spontanea. Purtroppo alla fine la teoria risultò fallimentare, ma ormai la strada era aperta: si cominciava a pensare alle dimensioni come a variabili, e non come a elementi fissi.

Si pensi però a come potrebbe esistere una dimensione extra senza essere percepibile ( Appendice: Flatlandia, E. Abbott). Non sempre la realtà è ciò che a noi è dato percepire. Come già propose il fisico svedese Klein, le dimensioni aggiuntive potrebbero essere "arrotolate" ed aver un diametro talmente piccolo da non essere rivelabili. Una ciambella (o toro) è una comune superficie a 2 dimensioni: se però facciamo restringere sempre di più il diametro della sezione trasversale, la ciambella sembra ridursi ad una circonferenza unidimensionale.

Dopo questo processo la 2° dimensione non è tuttavia scomparsa, si è semplicemente contratta, nascondendosi ai nostri sensi.

Allo stesso modo, le dimensioni extra sono compattificate in gomitoli dimensionali , presenti in ogni punto dello spaziotempo, dell'ordine della lunghezza di Planck(10^-33cm), impossibili quindi da rilevare sperimentalmente. Nell'ambito della teoria delle stringhe esse svolgerebbero un ruolo importante, in quanto la forma dei gomitoli determinerebbe diverse leggi presenti in natura. Dall'analisi dei fenomeni che avvengono nel nostro universo si è quindi cercato di stabilire quale sarebbe potuta essere la forma reale degli spazi di compattificazione. Tale titolo è stato conferito agli spazi di Calabi-Yau, spazi a 6 dimensioni provenienti dalla matematica.

Ciò tuttavia non rappresenta una meta, ma appena l'inizio di una lunga corsa. Esistono infatti infiniti spazi (o varietà) di Calabi-Yau associate ad ogni punto dello spazio-tempo. Gli scienziati hanno previsto decine di migliaia di possibili spazi di Calabi-Yau ammissibili dalla teoria delle stringhe; considerando che gli spazi potenziali candidati sono infiniti, si tratta di un gruppo molto ristretto.

La ricerca nel campo coinvolge inoltre numerosi procedimenti matematici: gli spazi di Calabi-Yau potrebbero infatti evolversi, unire estremi, lacerarsi, proprio come un pezzo di stoffa. Certamente risulta assai arduo immaginare strappi nella trama dello spazio tempo! È difficile immaginare dei fori nello spazio-tempo.

In realtà noi non avvertiamo gli effetti di tali trasformazioni in quanto le regioni in cui avviene lo strappo sarebbero isolate dal resto dello spazio-tempo, come da una campana di vetro. A svolgere tale ruolo è il foglio d'universo di una stringa, che, avvolgendo il foro, impedirebbe allo strappo di propagarsi.

Un'analogia molto usata è di considerare lo spazio multidimensionale come un tubo di gomma per il giardino. Se guardiamo il tubo da una certa distanza, esso sembra avere una sola dimensione, la sua lunghezza. In paragone ciò corrisponde alle 4 dimensioni macroscopiche cui siamo abituati normalmente. Se però ci avviciniamo al tubo, scopriamo che esso ha anche una seconda dimensione, la sua circonferenza. Questa dimensione extra è visibile solo se siamo vicini al tubo, proprio come le dimensioni extra degli spazi di Calabi-Yau sono visibili solo a distanze estremamente piccole e quindi non sono facilmente osservabili. (Ovviamente, un normale tubo per il giardino esiste nelle tre dimensioni spaziali, ma per consentire l'analogia si trascura il suo spessore e si considera solo il moto sulla superficie del tubo. Un punto sulla superficie del tubo può essere individuato con due numeri, la distanza da una delle estremità e una distanza sulla circonferenza, proprio come un punto sulla superficie terrestre può essere individuato univocamente dalla latitudine e dalla longitudine. In entrambi i casi, diciamo che l'oggetto ha due dimensioni spaziali.

Come la Terra, i tubi da giardino hanno un interno, una regione che richiede una dimensione extra; però, a differenza della Terra, uno spazio di Calabi-Yau non ha un interno).

6 IL "SUPER" DELLE SUPERSTRINGHE: Dualità e M-Teoria

Parlando di stringhe l'idea di Kaluza sembrerebbe a dir poco ottimistica: nei primi tempi queste piccole cordicelle sembravano stare davvero strette nelle nostre dimensioni, dal momento che la teoria per risultare coerente prevedeva un universo a 26 dimensioni, delle quali   compattificate in un consistente gomitolo dimensionale. 

Nonostante questo, le stringhe sembravano in grado di vibrare solo "note bosoniche[3]".

Fortunatamente tra queste risultava essere presente sempre una particella senza massa e con spin 2: queste sono le caratteristiche del gravitone, il quanto mediatore della forza di gravità tanto cercato nell'ambito del Modello Standard. La 4° interazione, rimasta fuori dal MS, risultava esser una componente fondamentale della teoria delle stringhe, il che era una bella conquista! 

Ma il carattere prettamente bosonico della teoria costituiva ugualmente un limite notevole: come spiegar l'esistenza delle particelle materiali, notoriamente fermioni[4]? A peggiorare le cose accanto al gravitone spuntarono numerosi stati  con energia negativa: i tachioni (particelle in grado di viaggiare più veloci della luce e con massa negativa). Tali particelle renderebbero il vuoto estremamente instabile e il mondo che ci circonda apparirebbe stravolto. La soluzione si doveva trovare eliminando i tachioni.

Dopo tante speranze, una possibile candidata al titolo di TOE non poteva sfumare per semplici particelle anomale! A questo punto entra in scena un'altra grande protagonista della fisica dei nostri tempi: la supersimmetria (SUSY).

Tale simmetria risulta avere una particolare importanza in quanto è in grado di correlare particelle con spin intero (bosoni) con particelle con spin semidispari (fermioni).

Così in un universo supersimmetrico ogni particella avrebbe un superpatner il cui spin differirebbe di mezza unità dal proprio.

La SUSY sembrava essere la soluzione: inserendola nella teoria i tachioni sparivano e portavano via con sé ben 16 delle dimensioni richieste, lasciando un universo a 10 dimensioni.  I problemi che affliggevano la teoria delle stringhe risultavano così risolti dalle "superstringhe".

La teoria delle stringhe che diventano super ha appassionato molti fisici che hanno riposto le proprie speranze in essa, ma che sembra ancora lungi dall'essere conclusa. 

Le stringhe, infatti, pur avendo molte caratteristiche di base in comune, possono differire per diversi particolari: avremo così stringhe aperte e stringhe chiuse, stringhe bosoniche e superstringhe, dimensioni e modi di vibrazione differenti. Una sola unità base ma diverse facce.

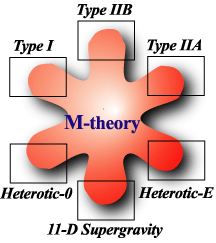
Questo si manifesta in una pluralità di teorie: in particolare nell'ambito delle stringhe supersimmetriche si individuano, oltre a quella bosonica a 26 dimensioni, 5 teorie fondamentali:

tipo I; tipo IIA; tipo IIB; tipo HO o SO(32); tipo HE o E₈ x E₈

Le varie tipologie di teoria possono essere legate da quella che è detta dualità, un particolare tipo di trasformazione, che permette di trasformare un tipo nell'altro attraverso vari passaggi.

"Purtroppo" abbiamo a disposizione un solo universo, per cui in ultima analisi si dovrebbe giungere alla definizione di una sola teoria.

Naturalmente questa non è la sola alternativa: potrebbero esistere infatti più universi, con caratteristiche diverse dal nostro in cui, ad esempio tra le forze da noi conosciute esista solo la gravità, ognuno descritto da una delle 5 teorie. Forse da qualche parte un fisico di un cosmo tipo IIA si sta chiedendo dove si troverà un universo di tipo I.

Il problema è ora capire quale tra le cinque 'candidate' vincerà l'ambito titolo di Teoria del Tutto. Forse tutte e. nessuna. Sembrerebbe proprio che in questo caso valga il detto 'l'importante è partecipare'. Non vi è infatti una teoria 'più vera' delle altre, ma una teoria derivante dalla sintesi di tutte le teorie di superstringa (tra cui è stata inserita anche la supergravità in 11 dimensioni), ribattezzata di recente M-teoria da Edward Witten. Il nome è un po' sui generis, proprio perchè la teoria non risulta totalmente definita: così può significare per teoria delle matrici, teoria madre, teoria del mistero e via dicendo. 

Gli abitanti di questo nuovo mondo non sarebbero però solo stringhe, ma anche membrane bidimensionali simili a piccoli frisbees. Perchè mai infatti la natura avendo a disposizione nove dimensioni avrebbe dovuto 'creare' solo oggetti unidimensionali? Al concetto classico di stringa viene così sostituito il concetto di p-BRANA, un 'nuovo' oggetto esteso in p-dimensioni (con p= 0-9). In quest'ottica una stringa apparirebbe come una 1-brana, una particella puntiforme come una 0-brana; e così come le stringhe (1-brane) muovendosi nello spazio determinano un foglio d'universo a 2 dimensioni, allo stesso modo una p-brana determinerà un volume d'universo a p+1 dimensioni.

Un altro punto a favore dell'M-teoria è l'unificazione di tutte le forze fondamentali, compresa la gravità, che finora è sfuggita a qualsiasi tentativo di unificazione. Sarebbe quindi l'M-teoria  la famigerata TOE (Theory of Everything), Teoria del Tutto, in grado di abbracciare in un'unica formulazione tutte le interazioni e le particelle presenti in natura? Purtroppo per ora si possono solo avanzare ipotesi. La matematica alla base della teoria è talmente complessa da consentire solo un primo approccio superficiale, che sembra però promettere bene