 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2058 | Gradito: |
Leggi anche appunti:Misure di potenza su linea trifase mediante inserzione RighiMisure di potenza su linea trifase mediante inserzione Righi Schema Introduzione al Base BleedIntroduzione al Base Bleed Una tra le tecniche piu` efficaci per La pressione nei fluidiLA PRESSIONE NEI FLUIDI Consideriamo una porzione di fluido in quiete contenuto |
 |
 |
Diffrazione da una fenditura
Innanzitutto consideriamo un esperimento: nella vaschetta delle onde liquide inviamo un'onda piana contro una larga apertura. Al di là dell'apertura l'onda procede quasi indisturbata e la larghezza del treno d'onde è grande circa come l'apertura stessa. L'ostacolo produce un'ombra ben riconoscibile. Solo ai lati dell'apertura si ha l'impressione che le superfici d'onda tendano a incurvarsi, come se delle deboli onde circolari nascessero dai bordi dell'apertura. Se stringiamo l'apertura quest'effetto diventa più appariscente. Quando poi l'apertura diventa larga come la lunghezza d'onda, allora al di là dell'ostacolo si propaga un'onda circolare e non si nota più nessuna ombra.
Il propagarsi dell'onda nella "zona dell'ombra geometrica" viene detto diffrazione. L'esperienza mostra che i fenomeni di diffrazione si osservano sempre quando l'apertura è dello stesso ordine di grandezza della lunghezza d'onda.


L'esperimento con la vaschetta delle onde liquide ci fornisce per analogia un'importante informazione ovvero la causa fondamentale della propagazione rettilinea della luce sta nella piccolezza della lunghezza d'onda. Infatti la lunghezza d'onda della luce è molto più piccola delle dimensioni degli oggetti con i quali abbiamo di solito a che fare, quindi i fenomeni di diffrazione sono praticamente trascurabili e le onde si propagano in linea retta e non nelle zone d'ombra.
Per verificare la nostra ipotesi consideriamo l'immagine dell'ombra prodotta da una stretta fenditura regolabile. Se vogliamo avere un'ombra nitida non dobbiamo illuminare direttamente la fenditura con un arco elettrico, ma dobbiamo usare un fascio di raggi più paralleli tra loro, possibilmente monocromatico.
Per ottenerlo poniamo davanti alla lampada ad arco un diaframma con una fenditura e un filtro rosso. Otteniamo così una sorgente luminosa rossa a forma di riga. Davanti a questa sistemiamo una lente convergente, in modo che il fuoco cada esattamente sulla fenditura del diaframma. Ora dalla lente esce un fascio di raggi paralleli rossi con i quali illuminiamo la fenditura regolabile e ne raccogliamo l'ombra su uno schermo lontano. Il dispositivo sperimentale si presenta come illustrato in figura.
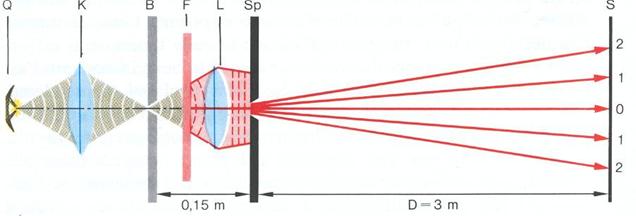

Se la fenditura è larga circa 1mm, allora i bordi dell'ombra appaiono nitidi. Ma se avviciniamo i due bordi della fenditura, cominciano ad apparire delle strisce chiare all'interno delle zone d'ombra ai bordi. Queste strisce sono così deboli che si possono vedere solo da vicino. Restringendo la fenditura fino a qualche centesimo di millimetro, esse si allargano e si espandono sempre di più nella zona d'ombra. Contemporaneamente anche i bordi dell'immagine vera e propria della fenditura si spostano, in modo che, al diminuire della fenditura, la sua immagine diventa sempre più larga. Siamo in presenza del fenomeno della diffrazione. Esso è una nuova prova della natura ondulatoria della luce.
Con le onde liquide generate nella vaschetta si è potuto vedere chiaramente solo il massimo centrale di diffrazione, quello detto di "ordine zero". I massimi laterali sono difficilmente visibili a causa della loro bassa intensità. Si confronti l'esperimento con le onde liquide e quello con le onde luminose, e si osservi che l'allargamento dell'immagine della fenditura, anche quando questa è estremamente stretta, rimane entro limiti modesti. Se ne deduce che la lunghezza d'onda della luce deve essere estremamente piccola, in ogni caso molto più piccola della larghezza della fenditura. Lo stesso esperimento ci dice anche quando si può parlare di raggio luminoso: la larghezza della fenditura deve essere molto maggiore della lunghezza d'onda della luce.


Diffrazione da una doppia fenditura
 Intorno al 1800 il medico inglese
Thomas Young riuscì a determinare per la prima volta la lunghezza d'onda della
luce. Per poter comprendere facilmente il suo procedimento ritorniamo alla
vaschetta delle onde liquide.
Intorno al 1800 il medico inglese
Thomas Young riuscì a determinare per la prima volta la lunghezza d'onda della
luce. Per poter comprendere facilmente il suo procedimento ritorniamo alla
vaschetta delle onde liquide.
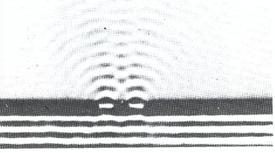
 Facciamo
passare un'onda piana attraverso due fenditure molto strette situate l'una
vicino all'altra. Dietro a ogni fenditura si propaga un'onda circolare. Queste
onde circolari si sovrappongono e danno luogo a una complicata figura di
interferenza. Dove una cresta si sovrappone a un'altra si ottiene una cresta
risultante di altezza doppia. Dove una concavità coincide con un'altra, si
ottiene una concavità risultante di profondità doppia. Viceversa, dove una
cresta si sovrappone a una concavità le onde si elidono reciprocamente. Questo
ultimo caso si verifica quando la differenza di cammino fra le due onde è pari
a un multiplo dispari di mezza lunghezza d'onda.
Facciamo
passare un'onda piana attraverso due fenditure molto strette situate l'una
vicino all'altra. Dietro a ogni fenditura si propaga un'onda circolare. Queste
onde circolari si sovrappongono e danno luogo a una complicata figura di
interferenza. Dove una cresta si sovrappone a un'altra si ottiene una cresta
risultante di altezza doppia. Dove una concavità coincide con un'altra, si
ottiene una concavità risultante di profondità doppia. Viceversa, dove una
cresta si sovrappone a una concavità le onde si elidono reciprocamente. Questo
ultimo caso si verifica quando la differenza di cammino fra le due onde è pari
a un multiplo dispari di mezza lunghezza d'onda.
 Vogliamo ora ripetere questo
esperimento con la luce. Utilizziamo il dispositivo adottato nell'esperienza
della diffrazione da una fenditura, sostituendo la fenditura regolabile con una
doppia. Sullo schermo compare un sistema di righe chiare e scure. Ci proponiamo
di determinare la posizione delle righe chiare. Consideriamo dapprima l'asse di
simmetria del dispositivo. In questa direzione le onde luminose si rafforzano
poiché percorrono lo stesso cammino. In coincidenza con l'asse si ha dunque una
zona di luce; è un risultato sorprendente, perché si sarebbe potuto pensare che
questa zona, coperta dall'ombra dello schermo tra le fenditure, avrebbe dovuto
essere scura.
Vogliamo ora ripetere questo
esperimento con la luce. Utilizziamo il dispositivo adottato nell'esperienza
della diffrazione da una fenditura, sostituendo la fenditura regolabile con una
doppia. Sullo schermo compare un sistema di righe chiare e scure. Ci proponiamo
di determinare la posizione delle righe chiare. Consideriamo dapprima l'asse di
simmetria del dispositivo. In questa direzione le onde luminose si rafforzano
poiché percorrono lo stesso cammino. In coincidenza con l'asse si ha dunque una
zona di luce; è un risultato sorprendente, perché si sarebbe potuto pensare che
questa zona, coperta dall'ombra dello schermo tra le fenditure, avrebbe dovuto
essere scura.
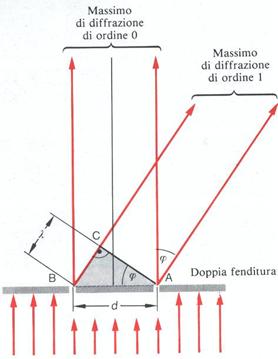
Consideriamo ora una direzione nel piano perpendicolare alle fenditure, che formi un angolo con l'asse di simmetria. Se l'angolo è tale che la differenza di cammino è esattamente uguale a una lunghezza d'onda, come avviene nella figura, le onde sovrapponendosi si rafforzano. Lo stesso avviene tutte le volte che il tratto BC è pari a un numero intero di lunghezze d'onda. Indicando con d la distanza fra le fenditure, si ottiene per l'angolo j

![]() con k=0,1,2,.
con k=0,1,2,.
Negli intervalli tra le direzioni che corrispondono a questi valori di j ve ne sono altre per cui la differenza di cammino fra le onde luminose è pari a un multiplo dispari di mezza lunghezza d'onda. Qui le onde si elidono reciprocamente e si ha oscurità. In definitiva si può dire:
in seguito alla diffrazione da una fenditura doppia si ottengono righe chiare, dette massimi di diffrazione di ordine k, la cui direzione è individuata dalla formula precedente.
Misurando la distanza d e l'angolo j si può determinare, sfruttando la figura di diffrazione, la lunghezza d'onda della luce, come fece Thomas Young nel 1802.
Diffrazione da un reticolo
 La figura di diffrazione ottenuta con
una doppia fenditura presenta tre grossi inconvenienti. I massimi di
diffrazione sono molto vicini fra loro, hanno deboli intensità e non hanno dei
contorni ben nitidi.
La figura di diffrazione ottenuta con
una doppia fenditura presenta tre grossi inconvenienti. I massimi di
diffrazione sono molto vicini fra loro, hanno deboli intensità e non hanno dei
contorni ben nitidi.
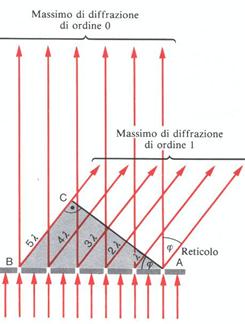
La formula precedente ci dice che la distanza tra i massimi di diffrazione cresce se avviciniamo le fenditure. Possiamo inoltre aumentare l'intensità dei massimi di diffrazione se facciamo sovrapporre non solo due treni d'onda ma un gran numero di questi. Sarà quindi opportuno usare molte fenditure disposte il più vicino possibile fra loro.
Si ottiene così un reticolo di diffrazione. La distanza fra due fenditure vicine è detta costante del reticolo.
 Come
mostra la figura, la posizione dei massimi di diffrazione viene fornita dalla
stessa formula della doppia fenditura. Più fenditure ha un reticolo, più nitidi
appaiono i massimi di diffrazione rispetto alle zone scure circostanti. Se
infatti la differenza di cammino fra due treni d'onda vicini differisce anche
solo di molto poco da un numero intero di lunghezze d'onda, passando da una
fenditura all'altra le differenze di cammino si sommano. Si può allora sempre
trovare un treno d'onde che, rispetto a quello considerato, è spostato di una
mezza lunghezza d'onda, e quindi lo distrugge per interferenza. Si passa così
repentinamente dal massimo di diffrazione all'oscurità.
Come
mostra la figura, la posizione dei massimi di diffrazione viene fornita dalla
stessa formula della doppia fenditura. Più fenditure ha un reticolo, più nitidi
appaiono i massimi di diffrazione rispetto alle zone scure circostanti. Se
infatti la differenza di cammino fra due treni d'onda vicini differisce anche
solo di molto poco da un numero intero di lunghezze d'onda, passando da una
fenditura all'altra le differenze di cammino si sommano. Si può allora sempre
trovare un treno d'onde che, rispetto a quello considerato, è spostato di una
mezza lunghezza d'onda, e quindi lo distrugge per interferenza. Si passa così
repentinamente dal massimo di diffrazione all'oscurità.
 Tuttavia la costante del reticolo d
non può essere resa troppo piccola. Infatti, se raggiungesse le dimensioni
della lunghezza d'onda, allora il massimo del primo ordine verrebbe diffratto
di 90° e i massimi di ordine superiore non comparirebbero più. Se poi fosse più
piccola della lunghezza d'onda, allora si potrebbe osservare solo il massimo di
diffrazione di ordine zero.
Tuttavia la costante del reticolo d
non può essere resa troppo piccola. Infatti, se raggiungesse le dimensioni
della lunghezza d'onda, allora il massimo del primo ordine verrebbe diffratto
di 90° e i massimi di ordine superiore non comparirebbero più. Se poi fosse più
piccola della lunghezza d'onda, allora si potrebbe osservare solo il massimo di
diffrazione di ordine zero.
Vogliamo ora misurare la lunghezza d'onda della luce con un reticolo. Per far ciò sostituiamo nel dispositivo del precedente paragrafo la doppia fenditura con un reticolo e togliamo il filtro rosso. Sullo schermo compare uno spettro di diffrazione simmetrico. Al centro troviamo il massimo di diffrazione di ordine zero. A sinistra e a destra i massimi del primo ordine. Poi i massimi del secondo ordine ecc. Il massimo di diffrazione di ordine zero è bianco, perché qui tutti i colori spettrali si sovrappongono. I massimi di diffrazione di ordine superiore sono rossi verso l'esterno e violetti verso l'interno. Confrontando questa disposizione cromatica con la nostra formula, vediamo che i vari colori spettrali sono disposti a seconda delle varie lunghezze d'onda, perciò luce di color rosso ha la lunghezza d'onda maggiore, quella violetta la lunghezza d'onda minore.
 Ora
vogliamo misurare la lunghezza d'onda della luce rossa, gialla, verde e blu con
un reticolo la cui costante vale d =
Ora
vogliamo misurare la lunghezza d'onda della luce rossa, gialla, verde e blu con
un reticolo la cui costante vale d =
![]()
Sostituendo quindi l'espressione appena trovata a senj nella formula della diffrazione da una doppia fenditura si ottiene:
![]()
Ecco i dati per i diversi colori.
|
Colore |
D (cm) |
S (cm) |
Sinj=s/D |
l=d*s/D (M) |
n=c/l (Hz) |
|
Rosso |
|
|
|
650E-09 |
4,6E14 |
|
Giallo |
|
|
|
580E-09 |
5,2E14 |
|
Verde |
|
|
|
530E-09 |
5,7E14 |
|
Blu |
|
|
|
480E-09 |
6,2E14 |

 Dalla tabella si nota che quando la
luce passa dal vuoto a un determinato mezzo, la sua frequenza rimane invariata
mentre la lunghezza d'onda diminuisce come la velocità. La grandezza che
caratterizza i singoli colori dello spettro è perciò la frequenza e non la
lunghezza d'onda. Diremo quindi che nel vuoto la velocità di propagazione è
indipendente dalla frequenza, mentre nella materia le onde luminose di
frequenza maggiore (blu) vanno più lente di quelle di frequenza minore (rosse).
Dalla tabella si nota che quando la
luce passa dal vuoto a un determinato mezzo, la sua frequenza rimane invariata
mentre la lunghezza d'onda diminuisce come la velocità. La grandezza che
caratterizza i singoli colori dello spettro è perciò la frequenza e non la
lunghezza d'onda. Diremo quindi che nel vuoto la velocità di propagazione è
indipendente dalla frequenza, mentre nella materia le onde luminose di
frequenza maggiore (blu) vanno più lente di quelle di frequenza minore (rosse).
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Biologia |  |
| Lezioni Chimica |  |