 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2940 | Gradito: |
Leggi anche appunti:La relativitÓ ristrettaLa relativitÓ ristretta Per descrivere un qualsiasi fenomeno fisico si deve Relazione di fisica - verifica sperimentale della legge del pendolo sempliceRELAZIONE DI FISICA -VERIFICA SPERIMENTALE DELLA LEGGE DEL PENDOLO SEMPLICE 1. CENNI Motore a combustione internaMotore a combustione interna Macchina termica motrice, in grado di trasformare |
 |
 |
╚ di estrema
importanza comprendere il significato concettuale della funzione d'onda.
L'interpretazione della funzione d'onda nasce da un'idea di Max Born, in
analogia con la teoria ondulatoria della luce, secondo la quale, il quadrato
dell'ampiezza di un'onda luminosa ha il significato di intensitÓ, che in
termini quantistici equivale al numero di fotoni presenti.
Cosý, mentre ψ pu˛ essere visto come ampiezza della funzione d'onda,
ψ2 esprime la probabilitÓ di trovare l'elettrone in un
determinato punto di coordinate x, y, z. Pi¨ esattamente, se in un punto r
(x,y,z) la funzione d'onda dell'elettrone ha ampiezza ψ, la probabilitÓ di
trovare l'elettrone nel volume infinitesimo Δv Ŕ proporzionale a
ψ2.
Per trasformare questa proporzionalitÓ in una uguaglianza Ŕ sufficiente
introdurre una adeguata costante di proporzionalitÓ, scelta in modo che la
somma delle singole probabilitÓ, estesa a tutto lo spazio, sia uguale a 1,
ovvero:
![]()
Questo procedimento si dice normalizzazione della funzione d'onda e C Ŕ la costante di normalizzazione.
Cerchiamo di comprendere nella maniera corretta i concetti che derivano dall'interpretazione di ψ2: lo faremo aiutandoci con un paio di grafici.
Per l'elettrone dell'atomo di H nello stato fondamentale, la funzione d'onda normalizzata Ŕ:
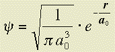
con a░ = 0.53 ┼ e r distanza dal nucleo.
Quindi, la probabilitÓ di trovare l'elettrone in un elemento di volume infinitesimo, a distanza r dal nucleo, Ŕ data da:
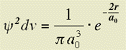
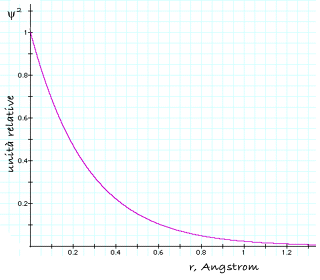
Il grafico di questa funzione, mostrato nella figura che segue, descrive la cosiddetta densitÓ di probabilitÓ elettronica. Come si pu˛ osservare, la densitÓ per unitÓ di volume Ŕ massima sul nucleo e decresce progressivamente allontanandosi da esso, fino a diventare zero a distanza infinita.
|
DensitÓ di probabilitÓ elettronica in funzione della distanza dal nucleo, per l'orbitale 1s dell'idrogeno |
╚ essenziale capire che tutto ci˛ non significa che la probabilitÓ di trovare l'elettrone sul nucleo Ŕ massima. Immaginiamo di scattare un'istantanea dell'atomo di idrogeno, nella quale l'elettrone appaia come un singolo punto localizzato in una determinata posizione. A che distanza dal nucleo Ŕ pi¨ probabile che si trovi questo punto? Se non riflettiamo attentamente sul significato 'geometrico' di ψ2, verrebbe quasi spontaneo rispondere 'a distanza zero, ovvero sul nucleo'. La risposta corretta Ŕ invece esattamente opposta: 'la probabilitÓ di trovare l'elettrone in un elemento di volume sul nucleo tende a zero'.
ψ2Δv
indica infatti la probabilitÓ riferita ad un elemento di volume infinitesimo
'centrato' in punti diversi lungo un'unica direzione, lungo un unico
raggio. Se confrontiamo un elemento di volume in prossimitÓ del nucleo con uno
identico lontano da esso, riscontriamo in effetti che Ŕ pi¨ probabile trovare
l'elettrone nell'elemento di volume pi¨ vicino al nucleo. Tuttavia, man mano
che ci allontaniamo dal nucleo, il numero degli elementi di volume cresce
proporzionalmente al quadrato della distanza (l'area di una superficie sferica
Ŕ data da 4π r2.
Quindi, Ŕ molto pi¨ indicativo considerare la funzione 4π r2
ψ2, detta funzione di distribuzione radiale, che
descrive la probabilitÓ di trovare l'elettrone su una superficie sferica (o
meglio, se moltiplicata per dr, entro un guscio sferico di spessore
infinitesimo dr) a distanza r dal nucleo. Dato che r2 aumenta in
modo quadratico al crescere del raggio, mentre ψ2 diminuisce,
la funzione di distribuzione radiale assume la forma illustrata nella Fig. 1.2,
dove si evidenzia un massimo che corrisponde al raggio pi¨ probabile, r=a░,
al quale si pu˛ incontrare l'elettrone intorno al nucleo. Per l'atomo di H
nello stato fondamentale questo valore coincide con il raggio di Bohr.
Tuttavia, piuttosto che enfatizzare l'analogia fra i due risultati, Ŕ
preferibile focalizzare la nostra riflessione sulla profonda differenza tra le
due teorie: in quella di Bohr l'elettrone si trova solo ad una distanza
definita dal nucleo, secondo la meccanica ondulatoria l'elettrone Ŕ invece del
tutto 'non localizzato' , ma si trova con maggior probabilitÓ
a distanza 0.53 ┼ dal nucleo.
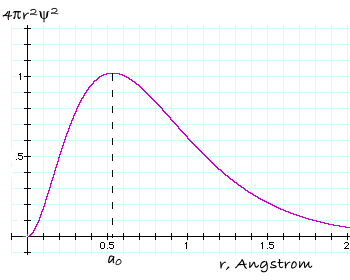
|
Funzione di distribuzione radiale in funzione della distanza dal nucleo, per l'orbitale 1s dell'idrogeno. La probabilitÓ di trovare l'elettrone Ŕ massima per r=ao ed Ŕ zero sul nucleo, dove il numero degli elementi di volume diventa infinitamente piccolo in confronto al numero di essi associato con valori di r maggiori. |
Il motivo per cui ho espressamente definito sferica la superficie di massima probabilitÓ Ŕ giustificato dal fatto che la funzione densitÓ di probabilitÓ Ŕ costante per ogni punto r equidistante dal nucleo, come mostra la figura. Ovvero, dipende esclusivamente da r ed Ŕ indipendente da una qualsiasi direzione: l'orbitale 1s dell'idrogeno ha infatti simmetria sferica.
Finora, ogni
volta che ci siamo riferiti all'elettrone, lo abbiamo fatto, probabilmente
anche inconsciamente, immaginandolo come una carica puntiforme negativa in
rapido movimento intorno al nucleo, ovvero pensando principalmente alla sua
natura corpuscolare discreta.
╚ tuttavia assai pi¨ conveniente, e avremo modo di capire in seguito quanto,
riuscire a 'costruirsi' un'immagine dell'elettrone nell'atomo, o
nelle molecole, come quella di una nuvola elettronica. Si pu˛ al limite,
con le dovute precauzioni, sovrapporre l'immagine della forma di un orbitale
atomico con quella dell'elettrone stesso (o, se Ŕ il caso, di una coppia di
elettroni). In sintesi, dobbiamo rappresentarci l'elettrone nell'atomo non pi¨
come una particella, ma come una superficie di distribuzione di una carica
diffusa. Questa superficie avrÓ la forma propria dell'orbitale e sarÓ pi¨ o
meno estesa intorno al proprio asse di simmetria, a seconda di quale
probabilitÓ di localizzare l'elettrone all'interno di essa vogliamo assegnarle
(ad esempio 90 o 95%).
Posta la questione in questi termini, sono giustificate, ed equivalenti, espressioni del tipo: 'l'elettrone passa il 95 % del proprio tempo all'interno di questa determinata superficie'; oppure, 'il 95% della carica elettronica Ŕ localizzato all'interno di quella determinata superficie'.
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Chimica |  |
| Lezioni Geografia |  |