 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 3302 | Gradito: |
Leggi anche appunti:Il Processo DryIl Processo Dry Il primo processo di realizzazione della doppia giunzione "Caratterizzazione (+)Limonane, a-Pinene, n-Ottene""Caratterizzazione (+)Limonane, a-Pinene, n-Ottene" Dati. Molecole con elettroni spaiati e paramagnetismoMolecole con elettroni spaiati e paramagnetismo Non sempre gli atomi utilizzano |
 |
 |
La maggior parte dei caratteri degli individui sono caratteri non mendeliani e manifestano pertanto una variabilità continua e non discreta. Si tratta in genere di caratteri tipicamente quantitativi come il peso, l'altezza, la forma del naso etc. Anche quando si tratta di caratteri numerabili (numero dei capelli) il numero delle classi numeriche è così elevato che la variabilità può comunque essere considerata continua.
L'ereditarietà di questi caratteri è più complessa rispetto ai caratteri mendeliani che si presentano in poche forme alternative ed in proporzioni caratteristiche. In particolare questi caratteri non si prestano ad essere selezionati. Se infatti si tenta di selezionare un particolare valore di un carattere continuo (ad esempio una pianta alta 1,50 cm all'interno di piante che presentano tutte le altezze comprese tra uno e due metri) segliendo nella progenie solo gli individui con quel valore ed incrociandoli, si ottengono sempre anche tutte le altre gradazioni.
Questo comportamento (non selezionabilità) aveva indotto i genetisti dell'inizio del '900 a ritenere che la variabilità di questi caratteri non avesse una base genetica, ma solo ambientale. Gli esperimenti condotti nei primi decenni del '900 dimostrarono che, oltre alla componente ambientale, tali caratteri presentano una base genetica di tipo poligenico, sono cioè caratteri controllati da numerosi geni (eredità poligenica).
Tutti i geni che controllano un carattere a variabilità continua presentano solo due tipi di alleli, detti fattori. Per questo motivo l'eredità poligenica è nota anche come eredità polifattoriale. I fattori possono essere solo di due tipi: fattori positivi (+) che spingono la manifestazione del carattere verso un estremo del suo intervallo di variabilità e fattori negativi (-) che spingono la manifestazione del carattere verso l'altro estremo del suo intervallo di variabilità. La manifestazione del carattere dipenderà dunque dalla particolare combinazione di fattori positivi e negativi.
I caratteri a variabilità continua presentano inoltre una particolare distribuzione di frequenza, nota come curva a campana o gaussiana.
Se ad esempio poniamo in ascissa le altezze della popolazione umana ed in ordinata la frequenza con cui gli individui di una determinata altezza compaiono nella popolazione, troveremo
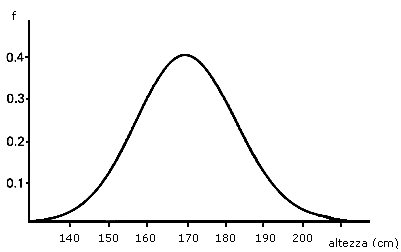
Gli individui che presentano i valori estremi del carattere (con tutti i fattori positivi o tutti i fattori negativi) sono molto rari, mentre avvicinandoci ai valori intermedi gli individui diventano sempre più frequenti.
Incrociando individui che si trovano agli estremi opposti dell'intervallo di variabilità si ottiene una progenie di individui con caratteri intermedi (regressione filiale). Incrociando gli individui intermedi la generazione successiva tende nuovamente a distribuirsi secondo una gaussiana.
Un esempio particolarmente semplice di eredità poligenica è rappresentato dal colore della cariosside del frumento, controllato da due soli geni. Il colore della cariosside dipende dalla quantità di pigmento presente e va dal rosso cupo al bianco attraverso 5 tonalità complessive di colore.
Se incrociamo due individui che stanno alle due estremità opposte dell'intervallo di variabilità, una pianta a semi rosso cupo (tutti e 4 i fattori positivi: genotipo ++ ++) con una pianta a semi bianchi (tutti e 4 i fattori negativi -- --) otterremo una pianta che riceverà ovviamente un gamete ++ da un genitore ed un gamete -- dall'altro. In F1 avremo pertanto un individuo dal colore intermedio, con due fattori positivi e due negativi (++ --).
Incrociando la progenie F1 e ipotizzando che i due geni possano ricombinarsi liberamente (assortimento indipendente) essi produrranno 4 tipi di gameti (++, +-, -+, --) che, posti ai due lati di un quadrato di Punnett, daranno 16 individui.
1 con quattro fattori positivi ++++
4 con tre fattori positivi ed uno negativo +++-
6 con due fattori positivi e due negativi ++--
4 con un fattori positivo e tre negativi +---
1 con quattro fattori negativi ----

Se riportiamo le 5 classi fenotipiche in un istogramma che ne evidenzi la distribuzione di frequenza, avremo

Come si può osservare due geni sono troppo pochi per ottenere una curva continua, ma l'aspetto è gia quello della distribuzione gaussiana.
Un carattere controllato da tre geni (6 fattori) presenta in F2 7 classi di frequenza. Per costruire la distribuzione di frequenza dovremmo incrociare un individuo con tutti e 6 i fattori positivi (++ ++ ++) con un individuo con tutti e 6 i fattori negativi (-- -- --). Ovviamente otterremo in F1 individui intermedi con tre fattori positivi e tre negativi (+- +- +-). Se incrociamo tra loro gli individui intermedi, nell'ipotesi che i fattori siano indipendenti e che quindi durante la gametogenesi vi sia una completa ricombinazione tra i fattori positivi e negativi, avremo 23 = 8 tipi di gameti (+++, ++-, +-+, +--, ---, --+, -+-, -++). Posizionando i gameti ai due lati di un quadrato di Punnett otterremo 8 x 8 = 64 combinazioni genotipiche.
È comunque possibile evitare di riempire il quadrato di Punnett e trovare la distribuzione di frequenza cercata, sviluppando la potenza pari di un binomio
(P + N)f
Dove
P = fattore positivo
N = fattore negativo
f = numero di fattori
Per 3 geni e quindi 6 fattori si ottiene
(P + N)6 = 1P6N0 + 6P5N1 + 15P4N2 + 20P3N3 + 15P2N4 + 6P1N5 + 1P0N6
i 7 monomi che si ottengono corrispondono alle 7 classi di frequenza, con i coefficienti dei monomi che corrispondono agli individui di ciascuna classe.
|
1P6N0 |
1 individuo con 6 fattori positivi |
|
++ ++ |
|
6P5N1 |
6 individui con 5 fattori positivi ed 1 negativo |
|
++ +- |
|
15P4N2 |
15 individui con 4 fattori positivi e 2 negativi |
|
++ -- |
|
20P3N3 |
20 individui con 3 fattori positivi e 3 negativi |
|
+- -- |
|
15P2N4 |
15 individui con 2 fattori positivi e 4 negativi |
|
-- -- |
|
6P1N5 |
6 individui con 1 fattore positivo e 5 negativi |
|
-- -- |
|
1P0N6 |
1 individuo con 6 fattori negativi |
|
-- -- |
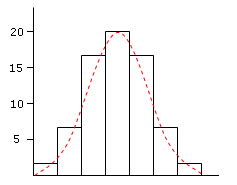
è evidente che al crescere del numero di fattori che controllano il carattere il numero di classi di variabilità aumenterà e l'istogramma sarà sempre più simile ad una curva.
 |
| Appunti su: caratteri non mendeliani, ereditC3A0 poligenetica appunti, variabilitC3A0 poligenica, caratteri mendeliani, ereditC3A0 poligenica chimica online, |
|
| Appunti Ingegneria tecnico |  |
| Tesine Geografia |  |
| Lezioni Biologia |  |